Question
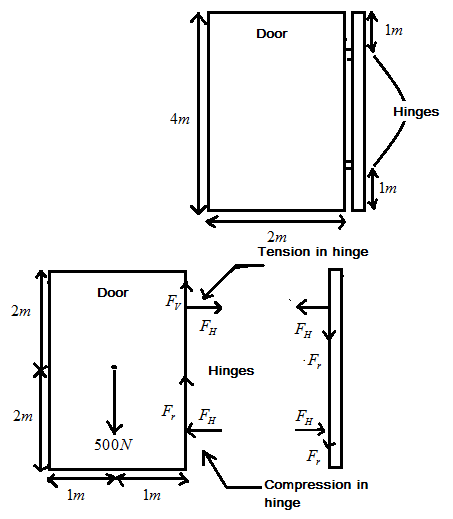
Question: The door of an almirah is \( 4m \) high, \( 1m \) wide and weighs \( 50kg \) . The door is supported...
The door of an almirah is 4m high, 1m wide and weighs 50kg . The door is supported by two hinges situated at a distance of 1m from the ends. If the magnitude of each force exerted by the hinges on the door is equal, find this magnitude.
Solution
Hint : Here, you are given a door of an almirah which is held vertically with the help of two hinges as supports. It is also given to you that the magnitude of each force exerted by the hinges on the door are equal. You are asked to find these forces exerted by the hinge. What you need to do is first draw the free body diagram of the forces that are acting on the door. To analyze the forces on the door and to get the values of them, you need to apply Newton’s law of motion and also, find torque if required.
Complete Step By Step Answer:
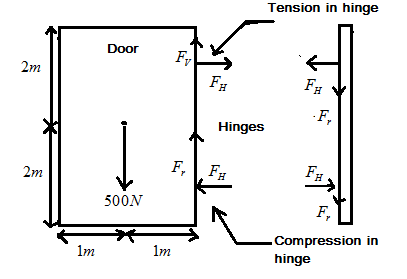
The free body diagram is made here. We denote the upper hinge as hinge 1 and the lower hinge as hinge 2.
The forces that will be applied by the hinge 1 are as follows:
(1) a force of magnitude FV=F1 acting vertically upward
(2) a force of magnitude FH=R1 acting towards the right.
The forces that will be applied by the hinge 2 are as follows:
(1) a force of magnitude FV=F2 acting vertically upward
(2) a force of magnitude FH=R2 acting towards the left.
Now, the door is obviously supposed to be in equilibrium and therefore the net force on the door is equal to zero. So, we have sum of vertical and sum of horizontal forces equal to zero. Let us write them in the form of equations.
F1+F2−(50)(10)=0 F1+F2=500
R1−R2=0 R1=R2
It is given to you that the magnitude of the force applied by the hinges are equal and therefore, we have,
F12+R12=F22+R22 F12+R12=F22+R22 F12+R12=F22+R12 ∴F12=F22 F1=F2
So, we get.
F1+F2=500 F1+F1=500 F1=F2=250N
Now, in order to get R1&R2 , we equate the torque about the hinge 2 to zero as the door does not rotate about that point with axis of rotation being perpendicular to the door, that is towards you. The door rotates only along the axis passing through both the hinges.
So, we get,
τhinge−2=(R1)(2)−(500)(1)=0 →R1=250N
As R1=R2 , we get R2=250N .
Therefore, the resultant force applied by a hinge is given as Fhinge=F12+R12=(250)2+(250)2=2502N Fhinge=353.55N
Hence, the magnitude of each force exerted by the hinges on the door is equal to 353.55N .
Note :
Here, we have used Newton’s second law of motion that the net force on the door is zero because the door is in equilibrium, meaning that the acceleration of the door is zero. Also, we used the torque about the hinge 2 in order to obtain the value of R1&R2 . So, you are supposed to keep in mind the approach we used to calculate the force applied by the hinges.
