Question

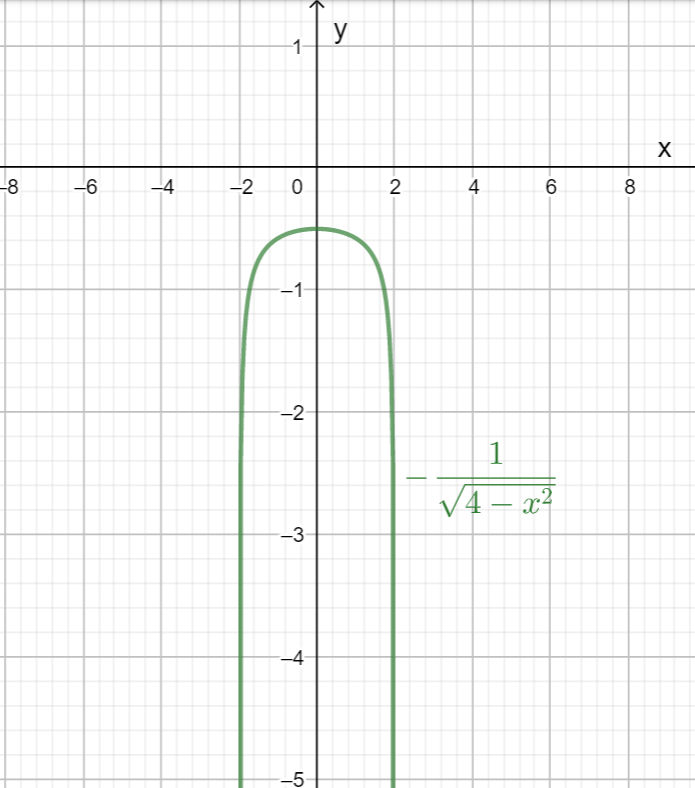
The domain of the real function $-\dfrac{1}{\sqrt{4-{{x}^{2}}}}$ is
1.The set of all real numbers
2. The set of all positive real numbers.
3. $\left( -2,2 \right)$
4. $\left[ -2,2 \right]$

Answer 1

In this problem, we have to find the domain of the given function. We can see that the denominator of the given function is greater than zero, so we can form an inequality and solve it to find the domain of the given function. We should know that the value of x should be a term, which should not make the denominator zero. We can now solve for x and find the domain value.

Complete step by step answer:
Here we have to find the domain of the given function,
$f\left( x \right)=-\dfrac{1}{\sqrt{4-{{x}^{2}}}}$
We can see that the denominator should be greater than zero.
We can now form an inequality, we get
$\Rightarrow \sqrt{4-{{x}^{2}}}>0$
We can now take square root on both sides, we get
$\Rightarrow 4-{{x}^{2}}>0$
We can now subtract 4 on both sides, we get
$\Rightarrow -{{x}^{2}}>-4$
We can now write the above step as,
$\Rightarrow {{x}^{2}}<4$
Taking square root on both sides, we get
$\Rightarrow x<\pm 2$

We can see that the value is less than, so we can conclude that we should not include the value of both positive and negative 2.
So, the correct answer is “Option 3”.

Note: We should always remember that if the resulting value is only less than, then we should not include them, so we can use the curve brackets. If the value is included as we have less than or equal to, then we can take the square brackets to denote them.