Question

The domain of the function $y = \sqrt {\sin x + \cos x} + \sqrt {7x - {x^2} - 6}$ is $\left[ {p,\dfrac{{q\pi }}{4}} \right] \cup \left[ {\dfrac{{r\pi }}{4},s} \right]$, then the value of p + q + r + s is

Answer 1

Hint – In this question first use the concept that the domain of square root is greater than equal to 0, thus $\sin x + \cos x \geqslant 0$ and $7x - {x^2} - 6 \geqslant 0$. For the terms involving trigonometric ratios convert them into the form $\sin \left( {A + B} \right)$ by multiplying and dividing $\sin x + \cos x \geqslant 0$ by $\sqrt 2$ . Solving the inequality will help to get the answer.

Complete step-by-step solution -
Given equation
$y = \sqrt {\sin x + \cos x} + \sqrt {7x - {x^2} - 6}$
Now to find out the domain the function which is in square root is always greater than or equal to zero.
$\Rightarrow \sin x + \cos x \geqslant 0$ ............. (1) and $7x - {x^2} - 6 \geqslant 0$........................... (2)
Now first solve first equation we have,
$\Rightarrow \sin x + \cos x \geqslant 0$
Now multiply and divide by $\sqrt 2$ we have,
$\Rightarrow \sqrt 2 \left( {\dfrac{1}{{\sqrt 2 }} \times \sin x + \dfrac{1}{{\sqrt 2 }} \times \cos x} \right) \geqslant 0$
Now as we know that $\sin {45^0} = \cos {45^0} = \dfrac{1}{{\sqrt 2 }}$
$\Rightarrow \sqrt 2 \left( {\cos 45 \times \sin x + \sin 45 \times \cos x} \right) \geqslant 0$
$\Rightarrow \left( {\cos {{45}^0} \times \sin x + \sin {{45}^0} \times \cos x} \right) \geqslant 0$
Now as we know that $\sin \left( {A + B} \right) = \sin A\cos B + \cos A\sin B$ so use this property in above equation we have,
$\Rightarrow \sin \left( {x + \dfrac{\pi }{4}} \right) \geqslant 0,{\text{ }}\left[ {\because {{45}^0} = \dfrac{\pi }{4}} \right]$
Now as we know $\sin x \geqslant 0,{\text{ }}x \in \left[ {0,\pi } \right],\left[ {2\pi ,3\pi } \right],....$
$\Rightarrow 0 \leqslant \left( {x + \dfrac{\pi }{4}} \right) \leqslant \pi$ and $2\pi \leqslant \left( {x + \dfrac{\pi }{4}} \right) \leqslant 3\pi$ .................
$\Rightarrow - \dfrac{\pi }{4} \leqslant x \leqslant \pi - \dfrac{\pi }{4}$ and $2\pi - \dfrac{\pi }{4} \leqslant x \leqslant 3\pi - \dfrac{\pi }{4}$ .................
$\Rightarrow - \dfrac{\pi }{4} \leqslant x \leqslant \dfrac{{3\pi }}{4}$ and $\dfrac{{7\pi }}{4} \leqslant x \leqslant \dfrac{{11\pi }}{4}$
$\Rightarrow x \in \left[ { - \dfrac{\pi }{4},\dfrac{{3\pi }}{4}} \right],\left[ {\dfrac{{7\pi }}{4},\dfrac{{11\pi }}{4}} \right]$................. (3)
Now consider equation (2) we have,
$\Rightarrow 7x - {x^2} - 6 \geqslant 0$
Now multiply by (-1) so the inequality sign reversed so we have,
$\Rightarrow - 7x + {x^2} + 6 \leqslant 0$
$\Rightarrow {x^2} - 7x + 6 \leqslant 0$
Now factorize this equation we have,
$\Rightarrow {x^2} - x - 6x + 6 \leqslant 0$
$\Rightarrow x\left( {x - 1} \right) - 6\left( {x - 1} \right) \leqslant 0$
$\Rightarrow \left( {x - 1} \right)\left( {x - 6} \right) \leqslant 0$
$\Rightarrow x \in \left[ {1,6} \right]$............................. (4)
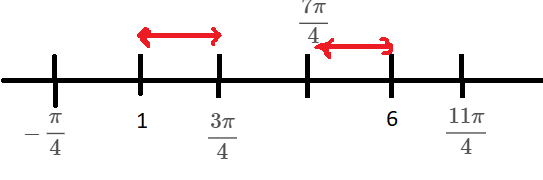
So the domain of the given equation is the intersection region of equation (3) and (4).
Now $\dfrac{{ - \pi }}{4} < 1$, $\dfrac{{3\pi }}{4} > 1$, $\dfrac{{7\pi }}{4} < 6$, $\dfrac{{11\pi }}{4} > 6$
Now the common region is shown in the above diagram so the domain of the given function is
$\Rightarrow \left[ {1,\dfrac{{3\pi }}{4}} \right] \cup \left[ {\dfrac{{7\pi }}{4},6} \right]$
So on comparing with $\left[ {p,\dfrac{{q\pi }}{4}} \right] \cup \left[ {\dfrac{{r\pi }}{4},s} \right]$
$\Rightarrow p = 1,q = 3,r = 7,s = 6$
So the value of p + q + r + s is
$\Rightarrow p + q + r + s = 1 + 3 + 7 + 6 = 17$
So this is the required answer.

Note – The domain of a function corresponds to the possible values of the independent variable that is x in this case, for which the entire function is defined. For example the domain of a quadratic function like $a{x^2} + bx + c = 0$ is $x \in R$ as this quadratic is defined for any value of x belonging to real axis from$- \infty {\text{ to }} + \infty$.