Question

The domain of the function $\sqrt{{{\log }_{0.5}}x}$ is
A. $(1,\infty )$
B. $(0,\infty )$
C. $\left( 0,1 \right)$
D. $\left( 0.5,1 \right)$

Answer 1

To find the domain of the function $\sqrt{{{\log }_{0.5}}x}$ , we will first consider the range of square functions. All square functions are always positive. Hence, ${{\log }_{0.5}}x\ge 0$ . From this, we will get a domain, that is, $\left[ -\infty ,1 \right]$ . Now for ${{\log }_{0.5}}x$ , $x> 0$ . So we will get $(0,\infty )$ . From these two, we will get the domain of $\sqrt{{{\log }_{0.5}}x}$ .

Complete step by step answer:
We need to find the domain of the function $\sqrt{{{\log }_{0.5}}x}$ .
We know that the square of a function is always positive. That is $\ge 0$ .
Hence, ${{\log }_{0.5}}x\ge 0$
Taking, anti-log, we will get $x\ge {{\left( 0.5 \right)}^{0}}$
We know that when $a$ ranges from $0< a< 1$ in ${{\log }_{a}}b$ , then $b< a$ . If $a> 1$ , then $b> a$ .
Here, $a=0.5$ that is less than $1$ . Hence the sign changes.
Therefore, $x\le {{\left( 0.5 \right)}^{0}}$ .
We know that ${{a}^{0}}=1$ . Therefore,
$x\le 1$
This is denoted as $\left[ -\infty ,1 \right]...(i)$
Now, we will consider ${{\log }_{0.5}}x$ . We know that the logarithm function is greater than $0$ .
Therefore, $x> 0$ .
This can be denoted as $(0,\infty )...(ii)$ .
Now let us find the domain from the plot below:

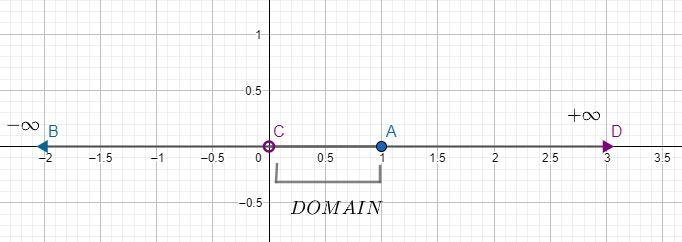
Hence, the domain is $(0,1)$ .

So, the correct answer is “Option C”.

Note: You will have to be very thorough with the rules of logarithm as we will be using these for questions of this type. You will have to consider the domain of square root function and the logarithmic function to obtain the required domain. Never forget to compare the domain to get a common domain.