Question

The domain of the function f\left( x \right)=\max \left\\{ \sin x,\cos x \right\\}\to \left( -\infty ,\infty \right) . The range of f(x) is?
a) $\left[ -\dfrac{1}{\sqrt{2}},1 \right]$
b) $\left[ -\dfrac{1}{\sqrt{2}},\dfrac{1}{\sqrt{2}} \right]$
c) [0, 1]
d) [-1, 1]

Answer 1

First look at definition of maximum function carefully. Now use the basic trigonometry knowledge to point the values of sin, cos at various angles, nearly 7-10 angles are needed. Try to point them in the range of $\left( -2\pi ,2\pi \right)$ as after it repeats the same graph. Now plot 7-10 points on a graph. By this you will have a graph of $\sin x,\cos x$ . Now apply the definition of maximum function to find a graph of maximum function, from this graph you can conclude the range. The range of this function is your result.

Complete step-by-step answer:
Maximum function: It is defined with the variable as 2 functions. At every x we check values of both the functions, take the value which is highest at particular.
Case-I: Plotting of graph of the sine function, $\sin x$ .
First we take the point as x = 0, by substituting this
$\sin x=\sin 0=0.................\left( i \right)$
By substituting the point as $x=\dfrac{\pi }{6}$ we get curve value as
$\sin x=\sin \dfrac{\pi }{6}=\dfrac{1}{2}.....................\left( ii \right)$
By substituting the point as $x=\dfrac{\pi }{4}$ we get curve value as
$\sin x=\sin \dfrac{\pi }{4}=\dfrac{1}{\sqrt{2}}...........................\left( iii \right)$
By substituting the value of $x=\dfrac{\pi }{3}$ we get value of curve as
$\sin x=\sin \dfrac{\pi }{3}=\dfrac{\sqrt{3}}{2}............................\left( iv \right)$
By substituting the value of $x=\dfrac{\pi }{2}$ we get value of curve as
$\sin x=\sin \dfrac{\pi }{2}=1.......................\left( v \right)$
By substituting ‘’- x’’ in place of x in all the above equations
$\begin{aligned} & \sin \left( -\dfrac{\pi }{6} \right)=-\dfrac{1}{2}.........................(vi) \\\ & \sin \left( -\dfrac{\pi }{4} \right)=-\dfrac{1}{\sqrt{2}}.......................\left( vii \right) \\\ & \sin \left( -\dfrac{\pi }{3} \right)=-\dfrac{\sqrt{3}}{2}........................\left( viii \right) \\\ & \sin \left( -\dfrac{\pi }{2} \right)=-1...........................\left( \text{ix} \right) \\\ \end{aligned}$
We know the range $\left( 0,\dfrac{\pi }{2} \right)$ repeats on $\left( \dfrac{\pi }{2},\pi \right)$ in reverse way and also the range $\left( 0,-\dfrac{\pi }{2} \right)$ repeats on $\left( -\dfrac{\pi }{2},-\pi \right)$ also in reverse. By plotting all the points with the conditions given we get,
Sin x:

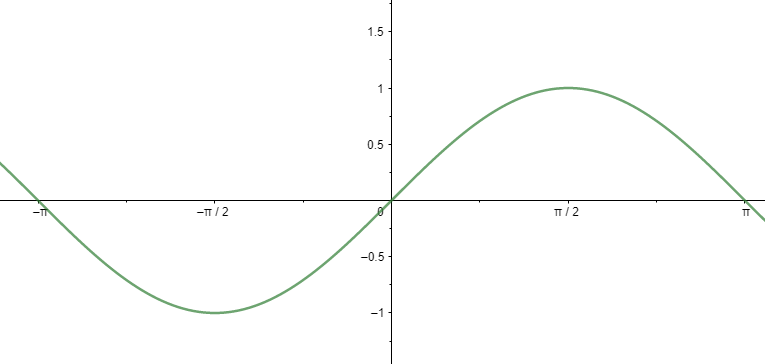
By repeating this plot we can generate $\sin x$ graph.
Case-II: For $\cos x$ graph we take the following plotting points by substituting the point x = 0, we get values of $\cos x$ as;
$\cos x=\cos 0=1...................\left( \text{x} \right)$
By substituting the point $x=\dfrac{\pi }{6}$ we get value of $\cos x$ as;
$\cos \left( x \right)=\cos \left( \dfrac{\pi }{6} \right)=\dfrac{\sqrt{3}}{2}........................\left( \text{xi} \right)$
Similarly for points $x=\dfrac{\pi }{4},x=\dfrac{\pi }{3},x=\dfrac{\pi }{2}$ we get value as
$\begin{aligned} & \cos \left( x \right)=\cos \left( \dfrac{\pi }{4} \right)=\dfrac{1}{\sqrt{2}}......................\left( \text{xii} \right) \\\ & \operatorname{cosx}=\cos \left( \dfrac{\pi }{3} \right)=\dfrac{1}{2}..........................\left( \text{xiii} \right) \\\ & \cos x=\cos \left( \dfrac{\pi }{2} \right)=0...........................\left( \text{xiv} \right) \\\ \end{aligned}$
We know in $\cos ,\cos \left( -x \right)=x$ so we can say that values as
$\begin{aligned} & \cos \left( \dfrac{-\pi }{6} \right)=\dfrac{\sqrt{3}}{2} \\\ & \cos \left( \dfrac{-\pi }{4} \right)=\dfrac{1}{\sqrt{2}} \\\ & \cos \left( \dfrac{-\pi }{3} \right)=\dfrac{1}{2} \\\ & \cos \left( \dfrac{-\pi }{2} \right)=0 \\\ \end{aligned}$
We know range $\left( \dfrac{\pi }{2},\pi \right)$ is same as $\left( \dfrac{-\pi }{2},0 \right)$ but reverse way similarly the range $\left( \dfrac{-\pi }{2},-\pi \right)$ is same as $\left( 0,\dfrac{\pi }{2} \right)$ but in reverse way by plotting all the points with above conditions we get
Cos x:

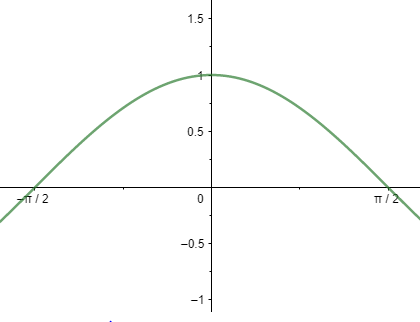
Now by combining the both graphs $\cos x,\sin x$ we get:

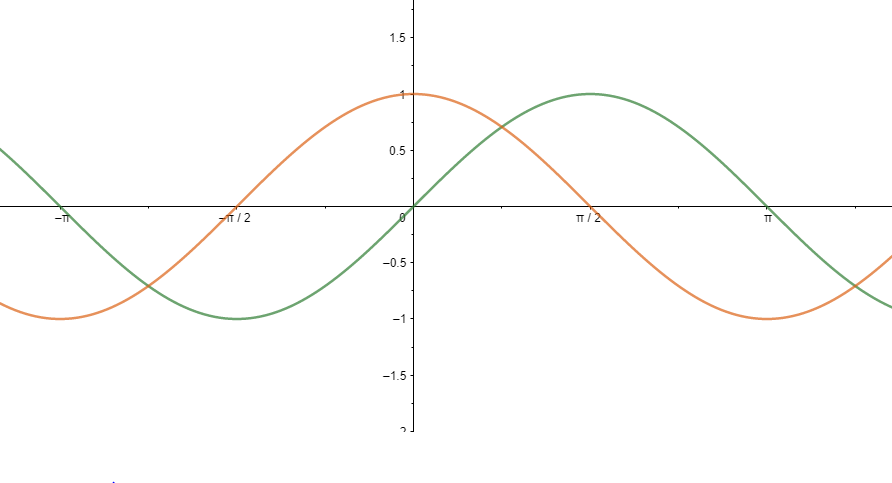
Now applying maximum function to each end every point

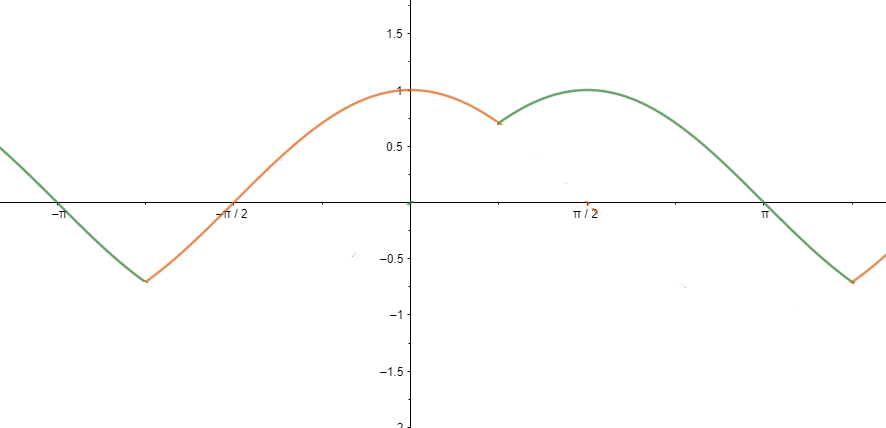
By looking at the graph we can say the range is $\left[ -\dfrac{1}{\sqrt{2}},1 \right]$ .

So, the correct answer is “Option a”.

Note: Be careful while plotting points because each and every point is important, if you miss one point you may mark an incorrect answer. The trick is to take the function graph which is above the other at every x.