Question

The domain of the definition of the function $f\left( x \right)=\dfrac{1}{4-{{x}^{2}}}+\log \left( {{x}^{3}}-x \right)$ is:
$\begin{aligned} & a.\left( 1,2 \right)\cup \left( 2,\infty \right) \\\ & b.\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 3,\infty \right) \\\ & c.\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 2,\infty \right) \\\ & d.\left( -2,-1 \right)\cup \left( -1,0 \right)\cup \left( 2,\infty \right) \\\ \end{aligned}$

Answer 1

The domain of the sum of two functions is given by the intersection of the domains of the two independent domains. So if $h\left( x \right)=f\left( x \right)+g\left( x \right)$, then the domain of $h\left( x \right)$ is given by ${{D}_{f}}\cap {{D}_{g}}$ where ${{D}_{f}}$ and ${{D}_{g}}$ are the domains of $f$ and $g$ respectively. We will use this concept to solve this question.

Complete step-by-step solution
Let us first find the domain of the function ${{h}_{1}}\left( x \right)=\dfrac{1}{4-{{x}^{2}}}$. Since the function is a rational function, the function is defined whenever the denominator is non - zero. Thus the domain of the function ${{h}_{1}}$ is given as follows,
{{D}_{{{h}_{1}}}}=\left\\{ x|4-{{x}^{2}}\ne 0 \right\\}=R-\left\\{ 2,-2 \right\\}
Now let us find the domain of the function ${{h}_{2}}\left( x \right)=\log \left( {{x}^{3}}-x \right)$. We know that $\log \left( y \right)$ is defined for all $y\in \left( 0,\infty \right)$. Thus for ${{h}_{2}}$ to be defined, ${{x}^{3}}-x>0$.
Let us factorize ${{x}^{3}}-x$. So, $x\left( {{x}^{2}}-1 \right)>0$.
$\Rightarrow x\left( x-1 \right)\left( x+1 \right)>0$.
Let us check the value of the function ${{x}^{3}}-x$ by substituting the values that were in the intervals $\left( -\infty ,-1 \right)$, $\left( -1,0 \right)$, $\left( 0,1 \right)$ and $\left( 1,\infty \right)$.
Let us substitute –2 in ${{x}^{3}}-x$.
So, we get ${{\left( -2 \right)}^{3}}-\left( -2 \right)=-6$.
Let us substitute $\dfrac{-1}{2}$ in ${{x}^{3}}-x$.
So, we get ${{\left( \dfrac{-1}{2} \right)}^{3}}-\left( \dfrac{-1}{2} \right)=\dfrac{3}{8}$.
Let us substitute $\dfrac{1}{2}$ in ${{x}^{3}}-x$.
So, we get ${{\left( \dfrac{1}{2} \right)}^{3}}-\left( \dfrac{1}{2} \right)=\dfrac{-3}{8}$.
Let us substitute 2 in ${{x}^{3}}-x$.
So, we get ${{\left( 2 \right)}^{3}}-2=6$.
We get the results as shown below.

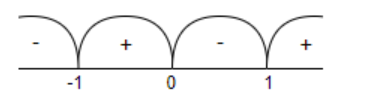
So, we get domain ${{D}_{{{h}_{2}}}}$ as $\left( -1,0 \right)\cup \left( 1,\infty \right)$.
We know that the domain of $f\left( x \right)={{h}_{1}}\left( x \right)+{{h}_{2}}\left( x \right)$ is given by ${{D}_{{{h}_{1}}}}\cap {{D}_{{{h}_{2}}}}$ which is given as follows,
\left( \left( -1,0 \right)\cup \left( 1,\infty \right) \right)\cap \left( R-\left\\{ -2,2 \right\\} \right)=\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 2,\infty \right)
Hence we get that the domain of $f\left( x \right)$ is given by,
$\left( -1,0 \right)\cup \left( 1,2 \right)\cup \left( 2,\infty \right)$
Hence, option (c) is the correct answer.

Note: One has to be very careful while solving the inequality ${{x}^{3}}-x>0$ because you need to consider both the positive and the negative values of x. Also, remember that the function $\dfrac{1}{x}$ is defined $\forall x\ne 0$. We can also draw the plot of ${{x}^{3}}-x$ to check where the curve is positive. Whenever we get this type of problem, we first solve for the domains of individual functions, and the intersection of domains is taken later to get the required domain.