Question
Question: The domain of $f(x) = log_{[\frac{x+1}{2}]}(x^2+x-2)$ is [Note: [k] denotes greatest integer functi...
The domain of f(x)=log[2x+1](x2+x−2) is
[Note: [k] denotes greatest integer function less than or equal to k.]
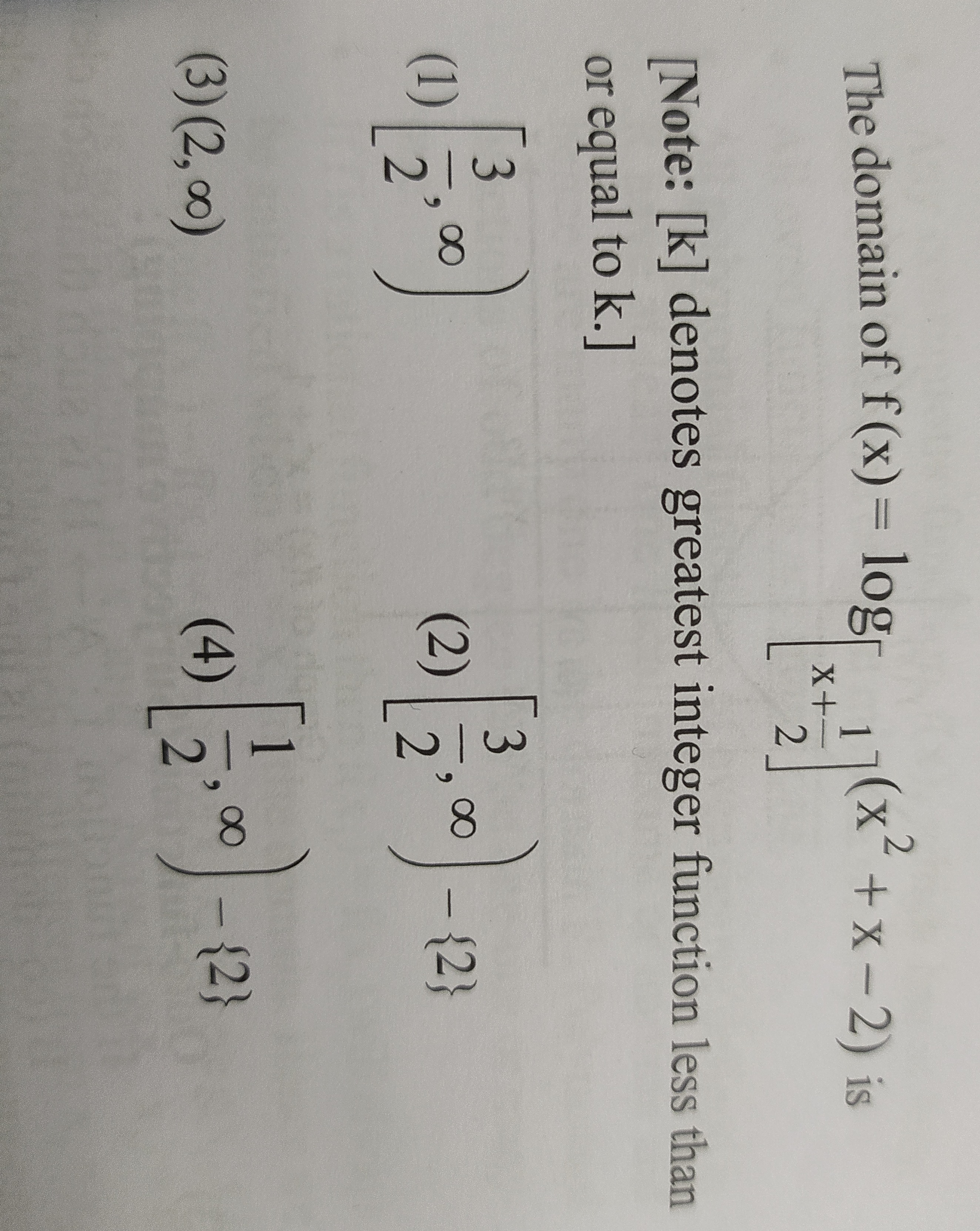
[23,∞)
[23,∞)−{2}
(2,∞)
[21,∞)−{2}
(2, \infty)
Solution
For the function f(x)=log[2x+1](x2+x−2) to be defined, the following conditions must be met:
-
The base must be positive: [2x+1]>0. The greatest integer function [k] is positive if and only if k≥1. So, 2x+1≥1⟹x+1≥2⟹x≥1.
-
The base must not be equal to 1: [2x+1]=1. The greatest integer function [k] is equal to 1 if and only if 1≤k<2. So, [2x+1]=1 if 1≤2x+1<2⟹2≤x+1<4⟹1≤x<3. Therefore, for [2x+1]=1, we must have x<1 or x≥3.
Combining conditions 1 and 2: We need x≥1 and (x<1 or x≥3). The intersection is x≥3. So, from the base conditions, x∈[3,∞).
- The argument must be positive: x2+x−2>0. Factor the quadratic expression: (x+2)(x−1)>0. This inequality holds when x is less than the smaller root or greater than the larger root. The roots are x=−2 and x=1. So, x<−2 or x>1.
Now, we need to find the intersection of the conditions from the base and the argument. We need x∈[3,∞) AND (x<−2 or x>1). The intersection of [3,∞) and (−∞,−2) is empty. The intersection of [3,∞) and (1,∞) is [3,∞). So, the domain is [3,∞).
Let's examine the given options: (1) [23,∞)=[1.5,∞) (2) [23,∞)−{2}=[1.5,∞)−{2} (3) (2,∞) (4) [21,∞)−{2}=[0.5,∞)−{2}
Our derived domain is [3,∞). Let's check if any option is equivalent to or contains [3,∞) while satisfying the conditions.
Consider option (3) (2,∞). If x∈(2,3), say x=2.5. Base: [22.5+1]=[23.5]=[1.75]=1. Argument: 2.52+2.5−2=6.25+2.5−2=6.75>0. The base is 1, so the logarithm is undefined. Thus, (2,3) is not in the domain. So, (2,∞) is not the correct domain.
