Question
Question: The distance \( x \) (in \( \mu m \) ) covered by the molecule starting from point A at time \( t = ...
The distance x (in μm ) covered by the molecule starting from point A at time t=0 and stopping at another Point B is given by the equation x=t2(2−3t) the distance between A and B ( in μm ) is closed to:
(A) 10.7
(B) 20.7
(C) 40.7
(D) 50.7
Solution
Here, we have been given the starting and ending point of the motion of molecule in a straight line and also the distance is given in the form of equation on solving this equation at time t we can be able to find the value of x . First from x find velocity of the particle and then the required distance would be easier to find.
Complete answer:
Here, the equation of distance between A and B is given by
x=t2(2−3t) …. (1)
Let us plot the points A and B, velocity at point B v=0
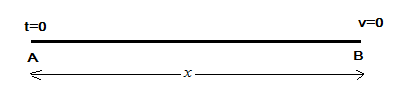
To find velocity of molecule at t is given by:
(1) ⇒ x=t2(2−3t)⇒x=2t2−3t3
v=dtdx
⇒v=dtd[2t2−3t3]
⇒v=4t−t2 ….. (2)
At point B; v=0
(2)⇒0=4t−t2
⇒t(4−t)=0
But, t=0
Hence, (4−t)=0
∴t=4sec
So, we have to put this value in equation (1) as:
eq(1)⇒x=(4)2(2−34)
⇒x=16(2−34)
⇒x=16×32
⇒x=10.67
Thus, here we have calculated the distance as 10.67μm
Precisely, it is 10.7μm
Therefore, the correct answer is option A.
Note:
Here, the distance is already given from that on differentiating it with respect to time we can calculate the velocity of the molecule. With the help of velocity we can calculate time and then the actual distance between two points of the movement of the molecule. Be careful about the concept used here and also have good calculation.
