Question

The distance of the moon from the earth is about $60$ times the radius of the earth. What will be the diameter of the earth (approximately in degrees) as seen from the moon?
A) ${1^ \circ }$

B) ${2^ \circ }$

C) ${4^ \circ }$

D) ${6^ \circ }$

Answer 1

Here we have to equate the length with radius times angle to get the answer. The parallax method is used to measure large distances. After getting the value in radian we have to convert it to degree.

Complete step by step solution:

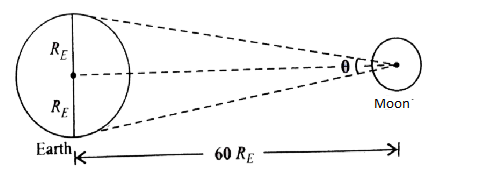
Let the radius of earth be ${R_E}$.
So, total distance will be $2{R_E}$ .
So, the distance between earth and moon will be $60{R_E}$ .
$\theta$ is the parallactic angle.
We know that,
$l = r\theta \\\ 2{R_E} = r\theta \\\ \theta = \dfrac{{2{R_E}}} {{60{R_E}}} = \dfrac{1} {{30}}\,rad \\\$

Since, we have to find the answer in degree.
So,
$\dfrac{1} {{30}} \times \dfrac{{180}} {\pi } \\\ = {2^ \circ } \\\$

Hence, the answer is option B.

Thus, the diameter of the earth (approximately in degrees) as seen from the moon is ${2^ \circ }$ .

Additional information:
Wide distances, such as the distance of a planet or a star from the earth, cannot be determined explicitly with a metre scale. A very important process-the parallax principle is used in those situations. When we place a pencil in front of us to a certain point on the back and first look at the pencil with our left eye (closing the left eye) and then staring at the pencil with the right eye (closing the left eye), we shall find that the location of the pencil appears to change with respect to the point on the wall. It is called parallax. This is the distance between the two observation points called the base. The base in this case is the distance between the eyes.

Note:
Here the distance will be twice the radius. If we only use ${R_E}$ then we will get a wrong answer. Also we have to convert the radian to degree by multiplying the answer with $\dfrac{{180}}{\pi }$ .