Question

The distance of point of a compound pendulum from its center of gravity is ${\text{ l, }}$ the time period of oscillation relative to this point is ${\text{ T}}{\text{. }}$ If ${\text{ g = }}{\pi ^2},{\text{ }}$ the relation between ${\text{ l }}$ and ${\text{ T }}$ will be:
A) ${l^2} - \left[ {\dfrac{{{T^2}}}{4}} \right]l + {k^2} = 0$
B) ${l^2} + \left[ {\dfrac{{{T^2}}}{4}} \right]l + {k^2} = 0$
C) ${l^2} - \left[ {\dfrac{{{T^2}}}{4}} \right]l - {k^2} = 0$
D) ${l^2} + \left[ {\dfrac{{{T^2}}}{4}} \right]l - {k^2} = 0$

Answer 1

A rigid body capable of oscillating about a horizontal axis passing through the pendulum is called a compound pendulum. If the pendulum rotates about a fixed point the distance between that fixed point and the center of gravity is the length of the pendulum. In this question, we have to find the relation between the length and the time period of oscillation.

Formula used:
$\tau = I\alpha$
Where, ${\text{ }}\tau {\text{ }}$is the torque of the pendulum, ${\text{ I }}$ is the moment of inertia of the pendulum and ${\text{ }}\alpha {\text{ }}$stands for the angular acceleration of the pendulum
$T = \dfrac{{2\pi }}{\omega }$
Where, ${\text{ T }}$ stands for the time period of the pendulum, ${\text{ }}\omega {\text{ }}$ stands for the angular velocity of the pendulum and ${\text{ 2}}\pi {\text{ }}$ is a constant
$\alpha = {\omega ^2}x$
Where ${\text{ }}\alpha {\text{ }}$ stands for angular acceleration, ${\text{ }}\omega {\text{ }}$ stands for angular velocity and ${\text{ x }}$stands for the displacement of the pendulum.

Complete step by step solution:
Consider the compound pendulum as shown in the figure:

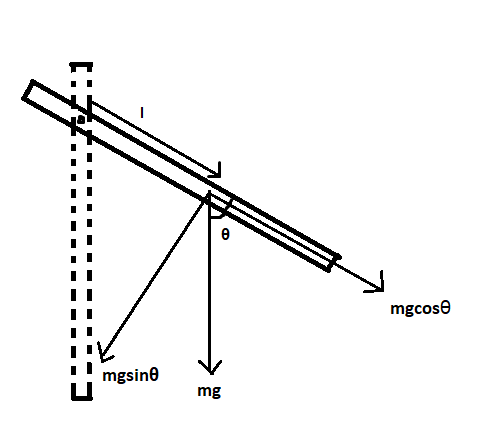
The weight${\text{ mg }}$is resolved into two components ${\text{ mg sin}}\theta$and${\text{ mg cos}}\theta {\text{ }}$.
The torque of the pendulum ${\text{ }}\tau = mgl\sin \theta$
When${\text{ }}\theta \to 0 \Rightarrow \sin \theta \approx \theta$
This implies
${\text{ }}\tau = mgl\theta$
We know that the torque,
${\text{ }}\tau {\text{ = I}}\alpha$
The length of the pendulum is${\text{ l }}$and the radius of gyration is given by${\text{ k }}$then the moment of Inertia ${\text{ }}\left( I \right){\text{ }}$of the pendulum is given by,
$I = m{k^2} + m{l^2}$
From equations and, we get
$\tau = mgl\theta = I\alpha$
From this equation we get
$\alpha = \dfrac{{mgl\theta }}{I}$ Substituting in equation
$\alpha = \dfrac{{mgl\theta }}{{m{k^2} + m{l^2}}} = \dfrac{{mgl\theta }}{{m({k^2} + {l^2})}} = \dfrac{{gl\theta }}{{({k^2} + {l^2})}}$
We know that the angular acceleration is also given by${\text{ }}\alpha = {\omega ^2}x$
Here the displacement${\text{ x }}$is the angular displacement${\text{ }}\theta {\text{ }}$
Therefore, the angular acceleration is,
$\alpha = {\omega ^2}\theta$
Equating and we get
${\omega ^2} = \dfrac{{gl}}{{({k^2} + {l^2})}}$
$\omega = \sqrt {\dfrac{{gl}}{{({l^2} + {k^2})}}}$
The time period of the pendulum is given by,
$T = \dfrac{{2\pi }}{\omega }$
Substituting the value of${\text{ }}\omega {\text{ }}$in, we get
$T = 2\pi \sqrt {\dfrac{{{l^2} + {k^2}}}{{gl}}} {\text{ }}$
It is given that,${\text{ g = }}{\pi ^2}$
Substituting this value we get
$T = 2\pi \sqrt {\dfrac{{{l^2} + {k^2}}}{{{\pi ^2}l}}} = 2\sqrt {\dfrac{{{l^2} + {k^2}}}{l}}$
Squaring both sides we get
${T^2} = 4\dfrac{{{l^2} + {k^2}}}{l}$
Rearranging the equation we get,
$\dfrac{{{T^2}}}{4} = \dfrac{{{l^2} + {k^2}}}{l}$
$\left( {\dfrac{{{T^2}}}{4}} \right)l = {l^2} + {k^2}$
${l^2} - \left( {\dfrac{{{T^2}}}{4}} \right)l - {k^2} = 0$

Therefore, The answer is Option (C) : ${l^2} - \left[ {\dfrac{{{T^2}}}{4}} \right]l - {k^2} = 0.$

Note: The radius of gyration of a body about an axis is defined as the radial distance to a point that would have a moment of inertia same as the distribution of mass of the body. The major difference between a simple pendulum and a compound pendulum is that in a simple pendulum the length of the pendulum i.e. the distance between the center of mass and the fixed point about which the pendulum is oscillating will be larger compared to that of a compound pendulum.