Question

The distance of a point P (a, b, c) from x-axis is
A. $\sqrt{{{b}^{2}}+{{c}^{2}}}$
B. $\sqrt{{{a}^{2}}+{{c}^{2}}}$
C. $\sqrt{{{b}^{2}}+{{a}^{2}}}$
D. a

Answer 1

Hint: The minimum distance between a point and a line is the perpendicular distance from that point to the line. A point is assumed on the line which is obtained on dropping a perpendicular from the given point on the line between which the distance is to be found out.

Complete Step-by-step answer:
As mentioned in the question, we have to find the distance between the point P (a, b, c) and the x-axis.
Now, on dropping a perpendicular from point P on the line, we get the point R (a, 0, 0).
Hence, the distance between the point P and the point R is the required distance and this is the distance between the point P and the x-axis.

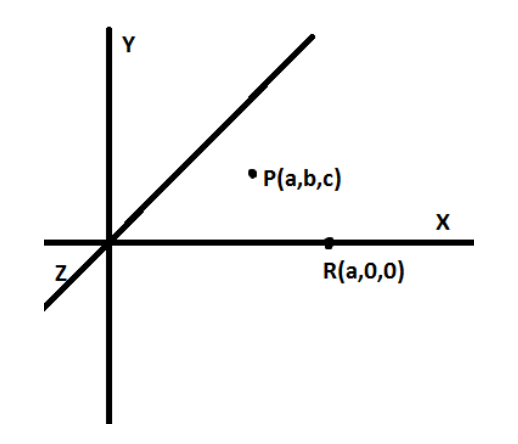
Hence, the distance between the points P and R is as follows

& =\sqrt{{{\left( a-a \right)}^{2}}+{{\left( b-0 \right)}^{2}}+{{\left( c-0 \right)}^{2}}} \\\ & =\sqrt{{{b}^{2}}+{{c}^{2}}} \\\ \end{aligned}$$ Hence, this is the required distance. Note: The students can make an error while evaluating the distance between the point P and the x-axis if they don’t incorporate the perpendicular distance method and try to solve the question with any other method because this method is the most precise one and cannot be solved otherwise.