Question
Question: The distance (m) vs. time (t) graph of a particle at \[t = 0\] makes an angle of \[45^\circ \] with ...
The distance (m) vs. time (t) graph of a particle at t=0 makes an angle of 45∘ with time axis. After 1 second it makes an angle of 60° with the time axis, what is the acceleration (in m/s2 ) of the particle, assuming its acceleration is constant for a given time period?
(A) 3−1
(B) 3+1
(C) 3
(D) 1
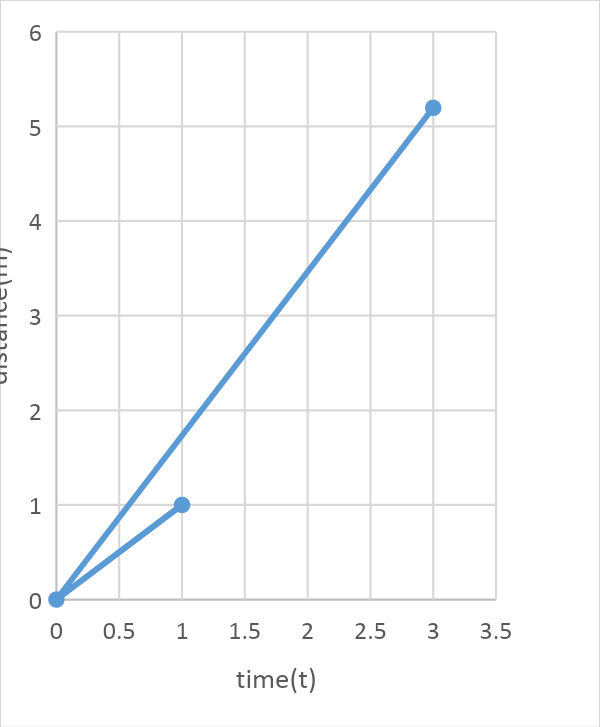
Solution
The slope of the distance time graph gives velocity. Find the velocity at two different time intervals by calculating the slope at that time. As acceleration is the ratio of change in velocity to time. Substitute the difference in velocities and the time interval to calculate the acceleration.
Complete step-by-step solution
Velocity of a moving body is given by dividing distance by time. In a distance time graph, the slope of the graph will give the velocity of that particle in that given time frame. The slope of a graph is also defined as the tangent of the angle the line makes with the x axis. As tan (angle) gives the quantity, y axis divided by x axis which is the slope of the graph.
For t=0 to t=1 ,
v0=tan(45)1
v0=1
For t>1
v1=tan(60)
v1=3
Acceleration is given by change in velocity divided by time, so
a=1v1−v0
a=3−1
Therefore, correct option is A
Note: During motion of a particle its parameters like velocity, position, and acceleration change with time. The slope of a distance time graph gives velocity of the body. Similarly, the slope of a velocity time graph gives acceleration. In a distance time graph the line is parallel to the time axis then the body is at rest. But for the velocity time graph it indicates that the body is moving with constant velocity.
