Question

The distance between two consecutive crests in a wave train produced on a string is 5cm. If two complete waves pass through any point per second, the velocity of the wave is
${\text{A}}{\text{. 10}}cm/s \\\ {\text{B}}{\text{. 2}}{\text{.5}}cm/s \\\ {\text{C}}{\text{. 5}}cm/s \\\ {\text{D}}{\text{. 15}}cm/s \\\$

Answer 1

The velocity of a wave is equal to the product of the frequency and the wavelength of the wave. The distance between two consecutive crests or troughs signifies the wavelength while the reciprocal to time period is the frequency of the wave.

Formula used:
The velocity of a wave is given as
${\text{v}} = \nu \lambda$
Here v is the velocity of the given wave, $\nu$ is the frequency of the given wave while $\lambda$ is the wavelength of the given wave.

Complete step by step answer:
A wave consists of a series of crests and troughs which repeat themselves after a fixed duration of time.
The distance between any two consecutive troughs or crests of a wave is known as the wavelength of the wave.

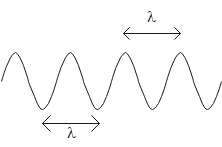
The number of times the wave crosses a point in a second is known as the frequency of the wave.
We are given that the distance between two consecutive crests in a wave train produced on a string is 5cm. This means that the wavelength of the wave is given as
$\lambda = 5cm$
We are also given that two complete waves pass through any point per second. This means that the frequency of the wave is given as
$\nu = 2Hz$
The velocity of a wave is equal to the product of the frequency of the wave and the wavelength of the wave. Therefore, the velocity of the given wave is given as
${\text{v}} = \nu \lambda = 2 \times 5 = 10cm/s$

So, the correct answer is “Option A”.

Note:
1. The wavelength of a wave can also be defined as the distance travelled by a wave in one time period. The time period of a wave can be defined as the time taken by a wave to repeat itself.
2. 1 hertz is given as $1Hz = 1{s^{ - 1}}$