Solveeit Logo
Login

Question

Question: The distance between two charges \(6\mu C\) and \(15\mu C\) is \(2m\) . At what point on the line jo...

The distance between two charges 6μC6\mu C and 15μC15\mu C is 2m2m . At what point on the line joining the two, the intensity will be zero?
A. At a distance 1m1m from 6μC6\mu C
B. At a distance 1m1m from 15μC15\mu C
C. At a distance 0.77m0.77m from 6μC6\mu C
D. At a distance 0.77m0.77m from 15μC15\mu C

Explanation

Solution

In order to solve this question we need to understand electric field and electric force. So electric field lines or electric fields are defined as the region around a charge in which if any other charge is placed then it experiences an electrical force either attractive or repulsive. We will calculate the electric field due to both charges and will solve for the point where net electric field intensity is zero.

Complete step by step answer:
Value of first charge be, q1{q_1} and it is equal to, q1=6μC{q_1} = 6\mu C
Value of second charge be, q2{q_2} and it is equal to, q2=15μC{q_2} = 15\mu C
Let the distance between them be, dd and it is given as, d=2md = 2m
Let at point P which is at a distance “x” from the first charge q1{q_1} , the intensity of the net electric field would be zero, as shown in figure.

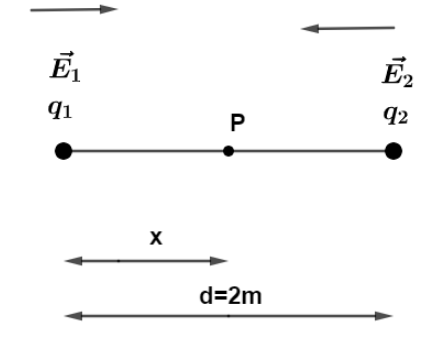
So electric field intensity from the first charge q1{q_1} at point P be, E⃗1=q14πε0(x)2x^{\vec E_1} = \dfrac{{{q_1}}}{{4\pi {\varepsilon _0}{{(x)}^2}}}\hat x it is in right direction.
Since the distance between second charge and point P is, d2=d−x{d_2} = d - x.
So electric field intensity from the first charge q2{q_2} at point P be, E⃗2=q24πε0(d2)2(−x^){\vec E_2} = \dfrac{{{q_2}}}{{4\pi {\varepsilon _0}{{({d_2})}^2}}}( - \hat x) it is in left direction
E⃗2=−q24πε0(d−x)2(x^){\vec E_2} = \dfrac{{ - {q_2}}}{{4\pi {\varepsilon _0}{{(d - x)}^2}}}(\hat x)
So net electric field at point P be,
E⃗=E⃗1+E⃗2\vec E = {\vec E_1} + {\vec E_2}
⇒E⃗=q14πε0(x)2x^+−q24πε0(d−x)2(x^)\Rightarrow \vec E = \dfrac{{{q_1}}}{{4\pi {\varepsilon _0}{{(x)}^2}}}\hat x + \dfrac{{ - {q_2}}}{{4\pi {\varepsilon _0}{{(d - x)}^2}}}(\hat x)
⇒E⃗=14πε0[q1x2−q2(d−x)2]x^\Rightarrow \vec E = \dfrac{1}{{4\pi {\varepsilon _0}}}[\dfrac{{{q_1}}}{{{x^2}}} - \dfrac{{{q_2}}}{{{{(d - x)}^2}}}]\hat x
Since net electric field is zero so,
E⃗=0\vec E = 0
⇒14πε0[q1x2−q2(d−x)2]x^=0\Rightarrow \dfrac{1}{{4\pi {\varepsilon _0}}}[\dfrac{{{q_1}}}{{{x^2}}} - \dfrac{{{q_2}}}{{{{(d - x)}^2}}}]\hat x = 0

Since constant cannot be zero, so
q1x2−q2(d−x)2=0\dfrac{{{q_1}}}{{{x^2}}} - \dfrac{{{q_2}}}{{{{(d - x)}^2}}} = 0
⇒d−xx=q2q1\Rightarrow \dfrac{{d - x}}{x} = \sqrt {\dfrac{{{q_2}}}{{{q_1}}}}
Putting values we get,
dx−1=156\dfrac{d}{x} - 1 = \sqrt {\dfrac{{15}}{6}}
⇒dx−1=1.58\Rightarrow \dfrac{d}{x} - 1 = 1.58
⇒dx=2.58\Rightarrow \dfrac{d}{x} = 2.58
⇒x=d2.58\Rightarrow x = \dfrac{d}{{2.58}}
Putting value of “d” we get,
x=22.58x = \dfrac{2}{{2.58}}
∴x=0.77m\therefore x = 0.77m

So, the correct option is C.

Note: It should be remembered that electric field intensity can only be zero in between the two charges and, because at any point between the two charges electric field due to both charge are in opposite direction, while at any point outside the distance, electric field intensity is not zero because field from both the charges are in same direction.