Question

The distance between the two charges $25\mu C$ and $36\mu C$ is $11\,cm$. At what point on the line joining the two, will the intensity be zero?
A. At a distance of $5cm$ from $25\mu C$
B. At a distance of $5cm$ from $36\mu C$
C. At a distance of $10cm$ from $25\mu C$
D. At a distance of $11cm$ from $36\mu C$

Answer 1

To answer this question we will first define an electric field and give its formula. Later we will draw a diagram exactly as stated in the question. Next we will apply the formula for electric field for both charges and equate them with each other to find the answer.

Formula used:
$E = k\dfrac{q}{{{r^2}}}$
Where, $q$ is the charge, $k$ is a constant with $8.99 \times {10^9}N{m^2}{C^{ - 2}}$ value and $r$ is the distance between charges.

Complete step by step answer:
Let us see what electric field intensity is: The electric field is the area around an electric charge where its impact can be felt. The force experienced by a unit positive charge put at a spot is the electric field intensity at that point.Look at the diagram:

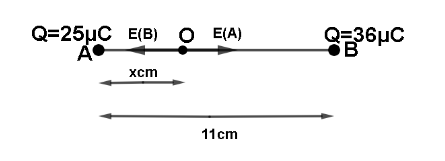
Let the charge at point A be $25\mu C$ and at B be $36\mu C$. Let O be the point where intensity is zero. It is at a distance ‘x’ from point A, then it is obvious that it is at a distance ‘11-x’ from point B.Now we will apply the equation individually for charge at A and charge at B.For charge at point A:
${E_A} = k\dfrac{{25 \times {{10}^{ - 6}}}}{{{x^2}}}$
Let this be equation 1
${E_A} = k\dfrac{{25 \times {{10}^{ - 6}}}}{{{x^2}}}.......(1)$
Now we will find at point B:
${E_B} = k\dfrac{{36 \times {{10}^{ - 6}}}}{{{{\left( {11 - x} \right)}^2}}}$
Let this be equation 2
${E_B} = k\dfrac{{36 \times {{10}^{ - 6}}}}{{{{\left( {11 - x} \right)}^2}}}.......(2)$

Now let us equate equations 1 and 2, we get:
${E_A} = {E_B}$
$\Rightarrow k\dfrac{{25 \times {{10}^{ - 6}}}}{{{x^2}}} = k\dfrac{{36 \times {{10}^{ - 6}}}}{{{{\left( {11 - x} \right)}^2}}}$
$\Rightarrow \dfrac{{25}}{{{x^2}}} = \dfrac{{36}}{{{{\left( {11 - x} \right)}^2}}}$
$\Rightarrow \dfrac{{{{\left( {11 - x} \right)}^2}}}{{{x^2}}} = \dfrac{{36}}{{25}}$
$\Rightarrow \dfrac{{\left( {11 - x} \right)}}{x} = \sqrt {\dfrac{{36}}{{25}}}$
Taking root on both sides
$\Rightarrow \dfrac{{\left( {11 - x} \right)}}{x} = \dfrac{6}{5}$
$\Rightarrow \left( {55 - 5x} \right) = 6x$
$\Rightarrow 55 = 6x + 5x$
$\Rightarrow 55 = 11x$
$\Rightarrow x = \dfrac{{55}}{{11}}$
$\therefore x = 5\,cm$
Hence the correct answer is that the intensity will be zero at a distance of $5cm$from $25\mu C$.

Hence the correct answer is option A.

Note: Students make a mistake while selecting a point where intensity is zero. In this question, to the left side of point A or right side of point B the intensity cannot be zero because at both these points intensities will add up as both are positive charges. Hence it will be zero only in between them.