Question

The distance between the tops of two trees 20m and 28m high is 17m. What is the horizontal distance between the two trees?
A 9 m
B 11 m
C 15 m
D 31 m

Answer 1

Hint: In this problem, first we need to draw the figure of the given situation. Next, find the length of side CE, by subtracting the height of the two trees. Now, apply Pythagoras theorem, to obtain the horizontal distance between the two trees.

Complete step-by-step answer:
Consider, the height of the 20m tree is AB, and the height of the 28 m tree is CD as shown below.

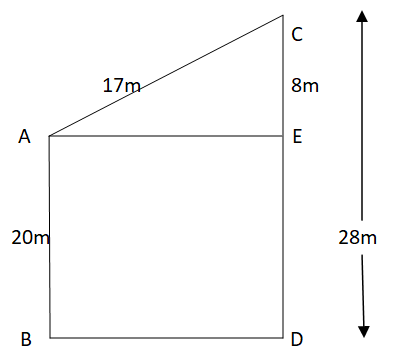
Here, the length AE is the horizontal distance between the two trees.
Now, apply the Pythagoras theorem in triangle ACE, to obtain the length AE as shown below.

\,\,\,\,\,\,A{C^2} = A{E^2} + E{C^2} \\\ \Rightarrow A{E^2} = A{C^2} - E{C^2} \\\ \Rightarrow AE = \sqrt {{{17}^2} - {8^2}} \\\ \Rightarrow AE = \sqrt {289 - 64} \\\ \Rightarrow AE = \sqrt {225} \\\ \Rightarrow AE = 15m \\\ \end{gathered}$$ Thus, the horizontal distance between two trees is 15m; hence, option (C) is the correct answer. Note: In this problem, the triangle ACE is a right angle triangle; hence, we can apply the Pythagoras theorem, in triangle ACE to obtain the length of side AE. Side AE represents the horizontal distance between the two trees.