Question

The distance between the point of suspension and the centre of gravity of a compound pendulum is $l$ and the radius of gyration about the horizontal axis through the centre of gravity is $k$, then its time period will be
A. $2\pi \sqrt {\dfrac{{l + k}}{g}}$
B. $2\pi \sqrt {\dfrac{{{l^2} + {k^2}}}{{lg}}}$
C. $2\pi \sqrt {\dfrac{{l + {k^2}}}{g}}$
D. $2\pi \sqrt {\dfrac{{2k}}{{lg}}}$

Answer 1

Obtain the equation of torque about point of suspension in terms of angular acceleration and momentum of inertia and it is also equal to force and perpendicular distance. Equation the equation obtained with general equation of motion, $\dfrac{{{d^2}\theta }}{{d{t^2}}} + {\omega ^2}\theta = 0$ where, $\dfrac{{{d^2}\theta }}{{d{t^2}}}$ is angular acceleration, $\theta$ is angular displacement and $\omega$ is the angular velocity.

Complete step by step answer:
From the given question, we know that the distance between the point of suspension (joint) and centre of gravity is $l$ and the radius of gyration is $k$. Let us consider the mass of the pendulum to be$m$. The figure below represents the pendulum at the horizontal position.

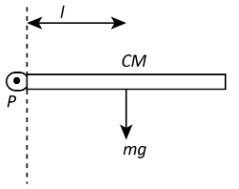
Let us obtain the torque about the point of suspension, the expression will be,
$T = \alpha {I_P}\\\ T = \dfrac{{{d^2}\theta }}{{d{t^2}}}{I_P}$ ... (i)
Here, $\alpha$ is the angular acceleration, $\theta$ is the angular displacement and ${I_P}$ is the moment of inertia about point $P$.
We know that the torque about the point of suspension can be written as,
$T = - mgl\sin \theta$
Here, $g$ is the acceleration due to gravity.
Substitute the expression in the above equation (i).
$\- mgl\sin \theta = \dfrac{{{d^2}\theta }}{{d{t^2}}}{I_P}\\\ \Rightarrow\dfrac{{{d^2}\theta }}{{d{t^2}}} + \dfrac{{mgl}}{{{I_P}}}\sin \theta = 0$
For small angle, $\sin \theta \approx \theta$, the above equation becomes,
$\dfrac{{{d^2}\theta }}{{d{t^2}}} + \dfrac{{mgl}}{{{I_P}}}\theta = 0$
On comparing with the general equation of motion, $\dfrac{{{d^2}\theta }}{{d{t^2}}} + {\omega ^2}\theta = 0$, we have,
$\omega = \sqrt {\dfrac{{mgI}}{{{I_P}}}}$
The moment of inertia about point P by using parallel axis theorem is,
${I_P} = {I_{CM}} + m{l^2}\\\ \Rightarrow{I_P} = m{k^2} + m{l^2}$
The time period of the pendulum is expression as,
$T = \dfrac{{2\pi }}{\omega }$
Substitute the expression in the given equation.

$$T = \dfrac{{2\pi }}{{\sqrt {\dfrac{{mgl}}{{m{k^2} + m{l^2}}}} }}\\\ \therefore T = 2\pi \sqrt {\dfrac{{{k^2} + {l^2}}}{{gl}}}$$

Thus, option C is correct.

Note: You should substitute the expression of moment of inertia at the point of suspension, not at the center of gravity because the torque is obtained at the point of suspension. Moment of inertia at point P can be obtained by using parallel axis theorem.According to this theorem, the moment of inertia at a point is equal to the sum of moment of inertia at CG and the product of mass and length between CG and that point.