Question

The distance between the chords of contact of tangents to the circle ${{\text{x}}^{\text{2}}}{\text{ + }}{{\text{y}}^{\text{2}}}{\text{ + 2gx + 2fy + c = 0}}$ from the origin and from the point (g,f) is-

Answer 1

Hint: To solve this question, we use the basic theory of circles. As given circle having equation: ${{\text{x}}^{\text{2}}}{\text{ + }}{{\text{y}}^{\text{2}}}{\text{ + 2gx + 2fy + c = 0}}$. First, we write the equation of tangent and chord to this circle and then after the tangent passes through origin, we put (0, 0) in this.

Complete step-by-step answer:

                                  ![](https://www.vedantu.com/question-sets/7685fa3e-b353-4b63-86f7-2957cedf3eb22111176030900056425.png)  

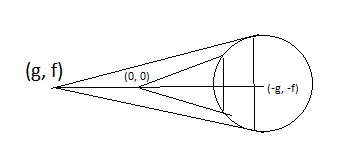
given equation of circle,
${{\text{x}}^{\text{2}}}{\text{ + }}{{\text{y}}^{\text{2}}}{\text{ + 2gx + 2fy + c = 0}}$.
Tangent to this circle at (p,q)
⇒xp+yq+g(x+p)+f(y+q)+c=0 …….... (1)
equations of chord of contact of tangents from origin (0,0) and point (g,f) given circle are,
⇒x(0)+y(0)+g(x+0)+f(y+0)+c=0
⇒gx+fy+c=0 ………... (2)
⇒xg+yf+g(x+g)+f(y+f)+c=0
⇒gx+fy+$\dfrac{{\text{1}}}{{\text{2}}}\left( {{{\text{g}}^{\text{2}}}{\text{ + }}{{\text{f}}^{\text{2}}}{\text{ + c}}} \right)$=0 ………. (3)
From (2) and (3) it's clear that equations are parallel.
Distance between these chords is given by,
= $\dfrac{{\dfrac{{\text{1}}}{{\text{2}}}\left( {{{\text{g}}^{\text{2}}}{\text{ + }}{{\text{f}}^{\text{2}}}{\text{ + c}}} \right){\text{ - c}}}}{{\sqrt {{{\text{g}}^{\text{2}}}{\text{ + }}{{\text{f}}^{\text{2}}}} }}$
= $\dfrac{{\left( {{{\text{g}}^{\text{2}}}{\text{ + }}{{\text{f}}^{\text{2}}}{\text{ + c}}} \right)}}{{2\sqrt {{{\text{g}}^{\text{2}}}{\text{ + }}{{\text{f}}^{\text{2}}}} }}$is the distance.
Therefore, The distance between the chords of contact of tangents to the circle ${{\text{x}}^{\text{2}}}{\text{ + }}{{\text{y}}^{\text{2}}}{\text{ + 2gx + 2fy + c = 0}}$ from the origin and from the point (g,f) is $\dfrac{{\left( {{{\text{g}}^{\text{2}}}{\text{ + }}{{\text{f}}^{\text{2}}}{\text{ + c}}} \right)}}{{2\sqrt {{{\text{g}}^{\text{2}}}{\text{ + }}{{\text{f}}^{\text{2}}}} }}$.

Note- Here are some basic properties of circles. For example, the outer line of a circle is at equidistant from the center. The diameter of the circle divides it into two equal parts. Circles which have equal radii are congruent to each other.