Question

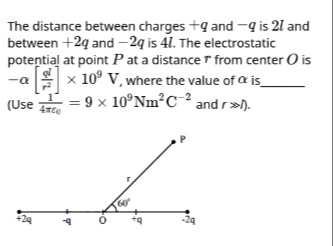
The distance between charges +q and -q is 2l and between +2q and -2q is 4l. The electrostatic potential at point P at a distance r from center O is $-\alpha \left[ \frac{ql}{r^2} \right] \times 10^9$ V, where the value of $\alpha$ is ______. (Use $\frac{1}{4\pi\epsilon_0} = 9 \times 10^9 Nm^2 C^{-2}$ and $r \gg l$).

Answer 1

27

Answer 2

The problem asks us to find the electrostatic potential at point P due to a system of four charges placed along the x-axis. We are given the positions of the charges relative to the origin O, and the coordinates of point P in polar form (distance r and angle $\theta = 60^\circ$). We are also given the condition $r \gg l$, which suggests using a multipole expansion for the potential.

Let the charges and their positions be:

1. Charge $Q_1 = +2q$ at $x_1 = -2l$
2. Charge $Q_2 = -q$ at $x_2 = -l$
3. Charge $Q_3 = +q$ at $x_3 = +l$
4. Charge $Q_4 = -2q$ at $x_4 = +2l$

The electrostatic potential $V$ at a point $(r, \theta)$ due to a system of charges $Q_i$ located at positions $x_i$ along the x-axis, for $r \gg x_i$, can be expressed using the multipole expansion: $V(r, \theta) = \frac{1}{4\pi\epsilon_0} \left[ \frac{\sum Q_i}{r} + \frac{(\sum Q_i x_i) \cos\theta}{r^2} + \frac{(\sum Q_i x_i^2) (3\cos^2\theta - 1)}{2r^3} + O(1/r^4) \right]$

Let's calculate the multipole moments:

1. Monopole moment (Total charge): $\sum Q_i = (+2q) + (-q) + (+q) + (-2q) = 0$

2. Dipole moment: $\sum Q_i x_i = (+2q)(-2l) + (-q)(-l) + (+q)(l) + (-2q)(2l)$ $= -4ql + ql + ql - 4ql$ $= -8ql + 2ql = -6ql$

3. Quadrupole moment: $\sum Q_i x_i^2 = (+2q)(-2l)^2 + (-q)(-l)^2 + (+q)(l)^2 + (-2q)(2l)^2$ $= (+2q)(4l^2) + (-q)(l^2) + (+q)(l^2) + (-2q)(4l^2)$ $= 8ql^2 - ql^2 + ql^2 - 8ql^2 = 0$

Now, substitute these values into the potential expansion. Since $\theta = 60^\circ$, we have $\cos\theta = \cos 60^\circ = 1/2$. Also, $3\cos^2\theta - 1 = 3(1/2)^2 - 1 = 3(1/4) - 1 = 3/4 - 1 = -1/4$.

Substituting the calculated moments and $\cos\theta$ into the potential formula: $V(r, 60^\circ) = \frac{1}{4\pi\epsilon_0} \left[ \frac{0}{r} + \frac{(-6ql)(1/2)}{r^2} + \frac{(0)(-1/4)}{2r^3} \right]$ $V(r, 60^\circ) = \frac{1}{4\pi\epsilon_0} \left[ -\frac{3ql}{r^2} \right]$

We are given that $\frac{1}{4\pi\epsilon_0} = 9 \times 10^9 \text{ Nm}^2 \text{ C}^{-2}$. So, $V = (9 \times 10^9) \left[ -\frac{3ql}{r^2} \right]$ V $V = -27 \left[ \frac{ql}{r^2} \right] \times 10^9$ V

The problem states that the electrostatic potential at point P is $-\alpha \left[ \frac{ql}{r^2} \right] \times 10^9$ V. Comparing our calculated potential with the given form: $-27 \left[ \frac{ql}{r^2} \right] \times 10^9 \text{ V} = -\alpha \left[ \frac{ql}{r^2} \right] \times 10^9 \text{ V}$

From this comparison, we can see that $\alpha = 27$.

The final answer is $\boxed{27}$.

Explanation of the solution:

1. Identify charges and their positions from the diagram.
2. Use multipole expansion for potential at a distant point ($r \gg l$).
3. Calculate monopole, dipole, and quadrupole moments of the charge distribution.
   • Monopole moment ($\sum Q_i$) = 0.
   • Dipole moment ($\sum Q_i x_i$) = -6ql.
   • Quadrupole moment ($\sum Q_i x_i^2$) = 0.
4. Substitute these moments and the given angle ($\theta = 60^\circ$) into the potential formula.
5. The potential simplifies to $V = \frac{1}{4\pi\epsilon_0} \left[ -\frac{3ql}{r^2} \right]$.
6. Substitute the value of $\frac{1}{4\pi\epsilon_0} = 9 \times 10^9$.
7. Compare the resulting potential expression with the given form $-\alpha \left[ \frac{ql}{r^2} \right] \times 10^9$ to find $\alpha$.