Question

The distance between an object and its real image produced by a converging lens is $0.72m$. The Magnitude of magnification is 2. What will be the magnitude of magnification when the object is moved by $0.04m$ towards the lens?
A. 2
B. 4
C. 3
D. 6

Answer 1

To solve the given problem we must know the formula for magnification due to a lens. Also we should know the lens equation. First use the magnification formula and given data to find v and u. Then find the focal length of the lens. Later, calculate the new position of the image. Then calculate the new magnification.

Formula used:
$|m|=\dfrac{|v|}{|u|}$
$\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$

Complete step by step answer:
Let the positions of the image and the object, with respect to the lens be v and u respectively.
The magnitude of magnification due a lens is given as $|m|=\dfrac{|v|}{|u|}$ ….. (i),
where, $|v|$ is the distance of the image and $|u|$ is the distance of the object form the lens.
It is given that the magnitude of magnification in the this case is 2. Therefore,
$\Rightarrow \dfrac{|v|}{|u|}=2$
$\Rightarrow |v|=2|u|$ …. (ii)
It is said that the image is real. This means that it is formed on the other side of the lens as shown in the figure.

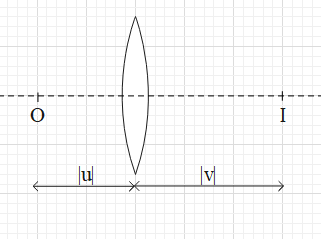
From the figure we get that the distance between the image and the object is $d=|v|+|u|$, And it is given that $d=0.72m$
$\Rightarrow |v|+|u|=0.72m$ …. (iii).
Substitute the value of the image distance from (ii).
$\Rightarrow 2|u|+|u|=0.72m$
$\Rightarrow |u|=\dfrac{0.72}{3}m=0.24m$.
And
$\Rightarrow |v|=2|u|=2\times 0.24=0.48m$.
This means that the object distance is $0.24m$ and the image distance is $0.48m$.
Let us assume that the object is a real object. For real objects, the value of u is always negative. Therefore, $u=-0.24m$.
And for real images, the value of v is positive. Therefore, $v=0.48m$.
Now, form the lens equation, i.e. $\dfrac{1}{f}=\dfrac{1}{v}-\dfrac{1}{u}$ (where f is the focal length of the lens) we get that $\dfrac{1}{f}=\dfrac{1}{0.48}-\dfrac{1}{-0.24}=\dfrac{3}{0.48}=\dfrac{1}{0.16}$.
$\Rightarrow f=0.16m$.
This means that the focal length of the lens is $f=0.16m$.
Then, it is said that the object is moved towards the lens by $0.04m$. Therefore, the new position of the object is $u'=-0.20m$.
Let us substitute the u’ and f in the lens equation to find the new position of the image (v’).
Therefore,
$\Rightarrow \dfrac{1}{0.16}=\dfrac{1}{v'}-\dfrac{1}{-0.2}$
$\Rightarrow \dfrac{1}{v'}=\dfrac{1}{0.16}-\dfrac{1}{0.2}=\dfrac{0.2}{0.16}=\dfrac{1}{0.8}$
$\Rightarrow v'=0.8m$.
This means that the new position of the image is $v'=0.8m$.
Further, we get that $|u'|=0.2m$ and $|v'|=0.8m$.
Substitute these values in (i).
$\Rightarrow |m|=\dfrac{0.8}{0.2}=4$.
Therefore, the magnitude of the new magnification is 4.

So, the correct answer is “Option B”.

Note:
Though in the given problem the value of magnification is considered to be positive, it can either be positive or negative depending on the values of u and v.
The actual definition of magnification is the ratio of the height of the image to the height of the
image formed.