Question

The distance between an object and a screen is 100cm. A lens produces an image on the screen when the lens is placed at either of the positions 40cm apart. The power of the lens is nearly
A.)3 diopter
B.)5 diopter
C.)2 diopter
D.)9 diopter

Answer 1

Hint: Recall the principle behind the displacement method. Then use the equation to find the focal length in terms of D and d, i.e. $f=\dfrac{{{D}^{2}}-{{d}^{2}}}{4D}$. Substitute the values of d and D in it. Find power using $P=\dfrac{1}{f}$ .

Complete step by step answer:
In a convex lens, the centre region is thicker compared to its edges. This lens is converging in nature; hence it is named as a converging lens. The light ray enters the lens undergo refraction and converges at a point called the principal focus, F. Then, the distance between the principal focus and the centre of the lens is the focal length. Reciprocal of the focal length is called the power of the length. Its unit is diopter.

To find the focal length and power of a thin convex lens, the displacement method of length is used. This is a simple method. The diagram is shown below.

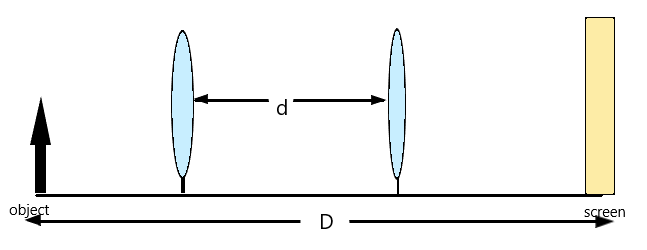
First, place the convex lens in front of an object, and then mark the distance at which the image formed as shown in the figure. Let us keep the position of the object and the screen fixed. Now move the lens slowly towards the screen till you get the clear image of the object. And after that point, the image starts to diminish. Fix the lens at that point.
The principle behind this is elementary. Even if we interchange the distance of an object towards the lens with the distance between image and lens, we will still get the image. Then the gap between the first and second position of the lens is taken as d, the displacement length.

Let us carefully look at the given problem. In the question, it stated that

The distance between the object and screen, D =100cm = 1m
The he displacement length of the lens, d = 40cm = 0.4m
Then the focal length is given by the formula,

$f=\dfrac{{{D}^{2}}-{{d}^{2}}}{4D}$
$f=\dfrac{{{1}^{2}}-{{(0.4)}^{2}}}{4\times 1}$
$f=\dfrac{1-0.16}{4}$
$f=\dfrac{.84}{4}$
$f=0.21$m

Therefore the power is given as $P=\dfrac{1}{f}$…………….(2)

Substituting the value of f in equation (2)

$P=\dfrac{1}{.21}$
$P=4.761diopter$
$P\approx 5diopter$

Therefore option B is the correct answer.

Note: The unit of power is generally written as diopter, $1diopter={}^{1}/{}_{m}$. This method is practical in the case of a thin lens. Always remember, in this method, the position of the object and the screen is always constant. Only the position of the lens is adjusted.