Question

The distance between 2$^{nd}$ crest and 6$^{th}$ trough of a wave shown below is 24cm. If the wave velocity of the moving crest is 20$m{{s}^{-1}}$, then frequency of rocking of the boat is

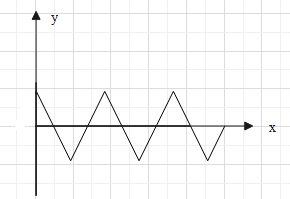
A. 24Hz
B. 20Hz
C. 375Hz
D. 240Hz

Answer 1

The distance two consecutive is equal to wavelength $\lambda$. Calculate the distance between 2$^{nd}$ crest and 6$^{th}$ trough in terms of the wavelength $\lambda$. Then use the formula $v=f\lambda$ to find the frequency of the boat.

Formula used:
$v=f\lambda$

Complete step by step answer:
In a wave, the maximum amplitude is called crest and the minimum amplitude is called trough. The distance between two consecutive crests or two consecutive troughs is equal to the wavelength ($\lambda$) of the wave.
At the middle of the distance between two consecutive crests lies a tough. The distance between the two crests is $\lambda$. Therefore, the distance between crest and its successive trough is $\dfrac{\lambda }{2}$.
Therefore, distance between the 2$^{nd}$ crest and 6$^{th}$ crest will be 4$\lambda$ and the distance between the 6$^{th}$ crest and the 6$^{th}$ will be $\lambda$. Hence, the total distance between the 2$^{nd}$ crest and 6$^{th}$ trough is $4\lambda +\dfrac{\lambda }{2}=\dfrac{9\lambda }{2}$.
And it is given that the distance between the 2$^{nd}$ crest and 6$^{th}$ trough is 24cm.
Therefore, $\dfrac{9\lambda }{2}=24cm$
$\Rightarrow \lambda =\dfrac{48}{9}=\dfrac{16}{3}cm=\dfrac{16}{3}\times {{10}^{-2}}m$.
Since, the boat is oscillating on the wave, the frequency of the boat will be equal to the frequency of the wave. Therefore, let us find the frequency of the wave. For this, we will use the formula $v=f\lambda$….(i), where f is the frequency and v is the speed of the wave.
It is given that the speed of the crest is 20$m{{s}^{-1}}$. Hence, the speed of the wave is 20$m{{s}^{-1}}$.
$\Rightarrow v=20m{{s}^{-1}}$
Substitute the values of $\lambda$ and v in equation (i).
$\Rightarrow 20=f\dfrac{16}{3}\times {{10}^{-2}}$
$\Rightarrow f=\dfrac{20\times 3\times {{10}^{2}}}{16}=\dfrac{1500}{4}=375Hz$
Therefore, the frequency of rocking of the boat is 375 Hz.
Hence, the correct answer is option C.

Note:
Sometimes, the question may ask to find the time period of oscillations. That time you may use the relation between time period and frequency of a wave. i.e. $T=\dfrac{1}{f}$.
We can also write the time period (T) in terms of wavelength since $f=\dfrac{v}{\lambda }$.
Therefore, $T=\dfrac{\lambda }{v}$.