Question

The dissociation of nitrogen pentoxide is a first-order reaction. In the first 24 min, 75% of nitrogen pentoxide is dissociated. What amount of nitrogen pentoxide will be left behind after one hour of the start of the reaction?
(A) Approximately 1 %
(B) Approximately 2 %
(C) Approximately 3 %
(D) None

Answer 1

A reaction that proceeds at a rate that depends linearly on only one reactant concentration is known as a first-order reaction. Other reactants can also be present in the reaction, but each will have zero order. The rate law and half-life for the first-order reaction are given below-
$-\dfrac{d[A]}{dt}=k[A]\text{; }{{\text{t}}_{1/2}}=\dfrac{\ln (2)}{k}$

Complete Solution:
-Calculating the half-life period of nitrogen pentoxide-

$\therefore {{t}_{1/2}} = \dfrac{24\min }{2}=12\min$
n = number of half-life in 1 hour (60 min) $= \dfrac{60}{12} = 5$

-Amount of substance left after 5 half-lives-
${{\left( \dfrac{1}{2} \right)}^{5}} = \dfrac{1}{32}$
Therefore, the % of the amount left $=\dfrac{100}{32}=3.125$

So, the correct answer is “Option C”.

Note: Let us see the derivation of half-life for first-order reactions-
The time taken for the concentration of a given reactant to reach 50% of its initial concentration is known as the half-life of a chemical reaction.
- For the first-order reaction, the rate constant can be mathematically given as –
$k=\dfrac{2.303}{t}\log \dfrac{[{{R}_{0}}]}{[R]}$

- From the definition of half-life,
At $t={{t}_{1/2}}$ and $[R]=\dfrac{[{{R}_{0}}]}{2}$

Substituting the above values in the equation for the first-order rate constant, we will get
$k=\dfrac{2.303}{{{t}_{1/2}}}\log \dfrac{[{{R}_{0}}]}{[{{R}_{0}}]/2}$

- Rearranging the above equation to get the value of ${{t}_{1/2}}$
${{t}_{1/2}}=\dfrac{2.303}{k}\log (2)$
As we know that the value of log(2) is 0.693.
Now, substituting the value of log 2 in the above equation, we will get,
${{t}_{1/2}}=\dfrac{0.693}{k}$

-Let us now see the graphs of the expected shapes of the curves for plots of reactant concentration versus time and the natural logarithm of reactant concentration versus time for a first-order reaction-

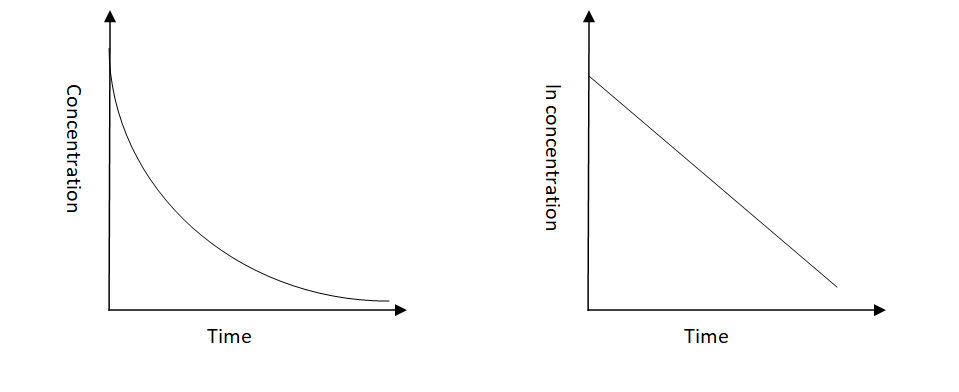
-The order for first-order reactions is always equal to 1. Following are some examples of first-order reactions-
(i) $S{{O}_{2}}C{{l}_{2}}\to C{{l}_{2}}+S{{O}_{2}}$
(ii) $2{{N}_{2}}{{O}_{5}}\to {{O}_{2}}+4N{{O}_{2}}$
(iii) $2{{H}_{2}}{{O}_{2}}\to 2{{H}_{2}}O+{{O}_{2}}$