Question

The displacement time graphs of particles A and B are straight lines making angles of ${{30}^{\circ }}\text{and }{{60}^{\circ }}$ respectively with the time axis. If the velocity of the particle A is ${{\text{v}}_{\text{A}}}$ and velocity of particle B is ${{\text{v}}_{\text{B}}}$, then the ration $\dfrac{{{\text{v}}_{\text{A}}}}{{{\text{v}}_{\text{B}}}}$ is,
A) $\dfrac{1}{2}$
B) $\dfrac{1}{\sqrt{3}}$
C) $\sqrt{3}$
D) $\dfrac{1}{3}$

Answer 1

Hint: We know that the velocity is the rate of change of displacement. So the slope of a displacement-time graph of a particle should give the velocity of the particle.

Complete step by step answer:

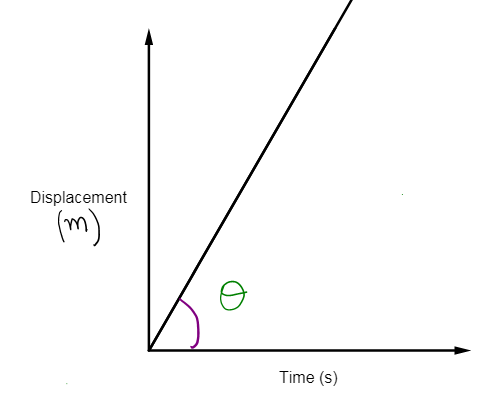
We know that in a displacement time graph, the velocity of the particle is given by the slope of the curve. If it is a straight line like in our case, the slope of the graph is given by the tangent of the angle between the line and the positive time axis. We can write it mathematically as,
$\text{Slope(m)}=\tan \theta$
Where, $\text{ }\\!\\!\theta\\!\\!\text{ }$ is the angle between the line and the time axis.
So if particle A makes an angle ${{30}^{\circ }}$ with the time axis, its velocity is given by the tangent of the angle, so the velocity of particle A is,
${{v}_{A}}=\tan \left( {{30}^{\circ }} \right)$
$\therefore {{\text{v}}_{\text{A}}}=\dfrac{1}{\sqrt{3}}$ ……equation (1)
So if particle B makes an angle ${{60}^{\circ }}$ with the time axis, its velocity is given by the tangent of the angle, so the velocity of particle B is,
${{v}_{B}}=\tan \left( {{60}^{\circ }} \right)$
$\therefore {{\text{v}}_{\text{B}}}=\sqrt{3}$ ……equation (2)

So from equation (1) and (2), we can find the required ratio,
$\dfrac{{{v}_{A}}}{{{v}_{B}}}=\dfrac{1/\sqrt{3}}{\sqrt{3}}$
$\therefore \dfrac{{{\text{v}}_{\text{A}}}}{{{\text{v}}_{\text{B}}}}=\dfrac{1}{3}$
So the correct option for the question is option (D)- $\dfrac{1}{3}$.

Note: The slope of a velocity-time graph will give the acceleration of a particle.
The area under the velocity-time graph will give the displacement of the particle.
The area under acceleration-time will give you the velocity of the particle.