Question
Question: The displacement time graph of two bodies \(A\) and \[B\] is shown in figure. The ratio of velocity ...
The displacement time graph of two bodies A and B is shown in figure. The ratio of velocity of A, vA to velocity of B, vB is
(A)31
(B)3
(C)31
(D)3
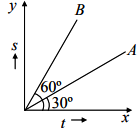
Solution
In this particular question, we will use the concept that the velocity is defined as the time rate of change of the displacement and this can also be expressed as the slope of the straight lines about the tangent of the inclination for a displacement time graph. By using this concept, we will get the velocities for the particles A and B respectively and then we will find the ratio.
Complete step by step answer:
In order to calculate the ratio of the two velocities, first we need to find the value of these two velocities.
We are all aware of the fact that the velocity is defined as the rate of change of the displacement with respect to the time and this is nothing but the slope of the straight lines about the tangent of the inclination.
So, we can say that,
v=dtdx=tanθ
The velocity of the particle A is,
vA=dtdxA
vA=tan30∘
vA=31.......(1)
Similarly, the velocity of the particle B is,
vB=dtdxB
vB=tan60∘
vB=3.......(2)
On dividing equation (1) and (2), we get,
vBvA=1331
vBvA=31
Hence, this is the required ratio of the velocities of particles A and B which are given in the question.
So, the final answer is (C)31.
Note: It is important to note that the slope of a straight line is basically the angle it makes with the positive direction of the x-axis in anticlockwise direction. Since v=dtdx so, the slope has a relationship with the velocity. Now, as acceleration is given by a=dtdv so, the slope of a velocity-time curve will give the value of acceleration.
