Question

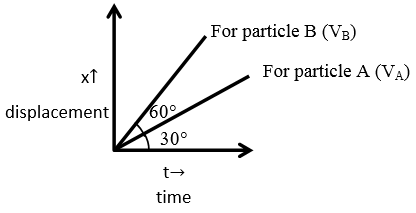
The displacement time graph of 2 particles A and B are straight lines making angles of respectively $30^\circ$ and $60^\circ$ with the time axis. If the velocity of A is ${v_A}$ and that of B is ${v_B}$, then the value of $\dfrac{{{v_A}}}{{{v_B}}}$ is
(A) $\dfrac{1}{2}$
(B) $\dfrac{1}{{\sqrt 3 }}$
(C) $\sqrt 3$
(D) $\dfrac{1}{3}$

Answer 1

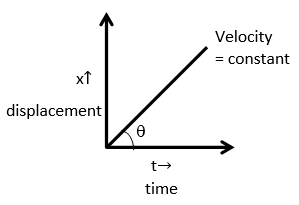
The slope of displacement-time graph represents the velocity.
Slope is given by $= \dfrac{{{x_2} - {x_1}}}{{{t_2} - {t_1}}}$
$= \dfrac{{dx}}{{dt}} = v(velocity)$
Slope is $\tan \theta =$ velocity

Complete step by step solution:
Velocity of any particle is defined as the ratio of displacement and time and the instantaneous velocity is defined as
$v = \dfrac{{dx}}{{dt}}$
which is also defined as the slope of the x-t curve.

i.e., slope $= \dfrac{{dx}}{{dt}} = v$ …..(1)
The slope of any curve is defined as
$\tan \theta =$ slope …..(2)
So, from equation (1) & (2)
$v = \tan \theta$
For particle A - ${v_A} = \tan {\theta _A}$
${\theta _A} = 30^\circ$
So, ${v_A} = \tan 30^\circ = \dfrac{1}{{\sqrt 3 }}$ …..(3)
For particle B - ${v_B} = \tan {\theta _B}$
${\theta _B} = 60^\circ$
${v_B} = \tan 60^\circ = \sqrt 3$ …..(4)
So, from equation (1)/(2)
$\dfrac{{{v_A}}}{{{v_B}}} = \dfrac{1}{{\sqrt 3 }} \times \dfrac{1}{{\sqrt 3 }} = \dfrac{1}{3}$
Hence $\dfrac{{{v_A}}}{{{v_B}}} = \dfrac{1}{3}$
So, option D is correct answer.

Note: Slope of x-t curve represents velocity $v = \dfrac{{dx}}{{dt}}$
Slope of v-t curve represents acceleration $a = \dfrac{{dv}}{{dt}}$
Area under v-t curve represents $\int {vdt = }$displacement