Question
Question: The displacement of center of mass of \( A + B \) system till the string becomes vertical is : ![]...
The displacement of center of mass of A+B system till the string becomes vertical is :
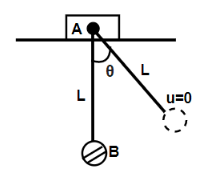
(A) zero
(B) 2L(1−cosθ)
(C) 2L(1−sinθ)
(D) None of these
Solution
This question will be solved by using the concept of center of mass. Firstly we will find the center of mass of the system when the point lies at C initially. And then when the string becomes vertical then also we will calculate at. Then for displacement we will subtract them.
Complete Step By Step Answer:
So let us assume the center of mass of the system lies at point C initially,
From the figure, we will get AD=Lcosθ
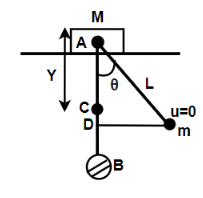
Therefore, the position of center of mass initially will be given by y=m+m0+m(AD)
Or we can write the above equation as
⇒y=2m0+m(Lcosθ)
On solving the above equation we get
⇒y=2Lcosθ
So now the string will become vertical and from the figure it will be represented as
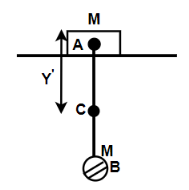
Therefore, the center of mass of the system will lies at the point called C
Hence, for this the position of center of mass finally will be given by y′=m+m0+m(AB)
Or we can write the above equation as
⇒y′=2m0+m(L)
On solving the above equation we get
⇒y′=2L
Now for the displacement of center of mass, it will be calculated by solving △y=y−y′
And on substituting the values, we will get the new equation as
⇒△y=2L−2Lcosθ
By taking the common, we get
⇒△y=2L(1−cosθ)
Hence, the displacement of the center of mass of the A+B system will be equal to 2L(1−cosθ) .
Note:
Center of mass is a point inside or outside an object which works as if the whole mass of the object is concentrated in that point. So in rigid body dynamic forces, all the points will keep their common distance complete and move as if one point follows the other. While solving the problems based on COM we should always keep the eye on, around which we are calculating as it makes a big difference when the position is different.
