Question

The directrix of a parabola is $x+8=0$ and its focus is at $\left( 4,3 \right)$ then the length of the latus rectum of the parabola is
(a) 5
(b) 9
(c) 10
(d) 12
(e) 24

Answer 1

We solve this problem by using the definition of a parabola to find the equation of the parabola. The rough diagram of the given parabola is

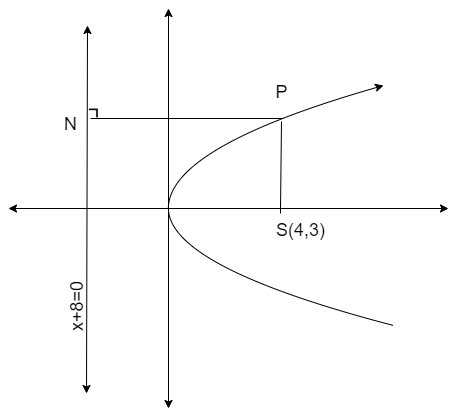
The definition of parabola says that the locus of points such that distance from the focus is equal to the perpendicular distance to the directrix. From the figure, the definition of parabola says that
$\Rightarrow SP=PN$
We use the distance formula between two points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given as
$AB=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
Also we use the perpendicular distance formula of point $A\left( {{x}_{1}},{{y}_{1}} \right)$ to line $ax+by+c=0$ is given as
$D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
By using the above formulas we find the equation of parabola so that we can get a latus rectum easily.

Complete step by step solution:
We are given that the equation of directrix as
$\Rightarrow x+8=0$
We are given that the focus of parabola as $S\left( 4,3 \right)$
Let us assume that there is a point $P\left( x,y \right)$ on the parabola.
We know that the definition of parabola says that the locus of points such that distance from the focus is equal to the perpendicular distance to the directrix. From the figure the definition of parabola says that
$\Rightarrow SP=PN.......equation(i)$
We know that the distance formula between two points $A\left( {{x}_{1}},{{y}_{1}} \right),B\left( {{x}_{2}},{{y}_{2}} \right)$ is given as
$AB=\sqrt{{{\left( {{x}_{2}}-{{x}_{1}} \right)}^{2}}+{{\left( {{y}_{2}}-{{y}_{1}} \right)}^{2}}}$
By using the above formula we get the distance SP as
$\Rightarrow SP=\sqrt{{{\left( x-4 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}$
Now, we know that the perpendicular distance formula of point $A\left( {{x}_{1}},{{y}_{1}} \right)$ to line $ax+by+c=0$ is given as
$D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$
By using the above formula we get the distance PN as

& \Rightarrow PN=\dfrac{\left| x+8 \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \\\ & \Rightarrow PN=\left| x+8 \right| \\\ \end{aligned}$$ Now, by substituting the values of SP and PN in equation (i) we get $$\Rightarrow \sqrt{{{\left( x-4 \right)}^{2}}+{{\left( y-3 \right)}^{2}}}=\left| x+8 \right|$$ Now, by squaring on both sides we get $$\begin{aligned} & \Rightarrow {{x}^{2}}-8x+16+{{\left( y-3 \right)}^{2}}={{x}^{2}}+16x+64 \\\ & \Rightarrow {{\left( y-3 \right)}^{2}}=24x+48 \\\ \end{aligned}$$ Now, by taking the common term out from RHS we get $$\Rightarrow {{\left( y-3 \right)}^{2}}=24\left( x+2 \right)$$ We know that if the equation of parabola is of the form $${{\left( y-a \right)}^{2}}=4b\left( x-c \right)$$ then the length of latus rectum is $$'4b'$$ By using this theorem to the equation of parabola we get $$\Rightarrow \text{Latus rectum}=24$$ Therefore the length of the latus rectum of a given parabola is 24. **So, option (e) is the correct answer.** **Note:** We have a shortcut for this problem. The length of latus rectum of parabola is twice the perpendicular distance from focua to directrix that is $$\Rightarrow \text{Latus rectum}=2\left( \text{Perpendicular distance from focus to directrix} \right)$$ We know that the perpendicular distance formula of point $$A\left( {{x}_{1}},{{y}_{1}} \right)$$ to line $$ax+by+c=0$$ is given as $$D=\dfrac{\left| a{{x}_{1}}+b{{y}_{1}}+c \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$$ By using the above formula we get the distance latus rectum as $$\begin{aligned} & \Rightarrow \text{Latus rectum}=2\left( \dfrac{\left| 4+8 \right|}{\sqrt{{{1}^{2}}+{{0}^{2}}}} \right) \\\ & \Rightarrow \text{Latus rectum}=2\times 12=24 \\\ \end{aligned}$$ Therefore the length of the latus rectum of a given parabola is 24.