Question
Question: The diode shown in the circuit given below has a constant voltage drop of \(0.6V\) at all currents a...
The diode shown in the circuit given below has a constant voltage drop of 0.6V at all currents and a maximum power rating of 300 milliwatt. What should be the value of the resistance R, if maximum current passes through the diode?
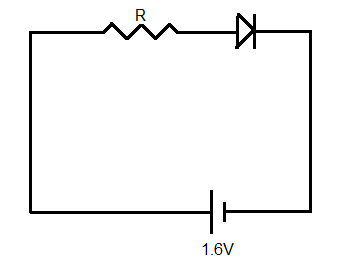
A) 4Ω
B) 2Ω
C) 1Ω
D) 32Ω
Solution
This problem can be solved by finding out the maximum current that can travel through the diode from the power rating given. After that we can find out the voltage drop across the resistor and the diode and apply Kirchhoff’s voltage law for the loop and get a value for the resistance.
Formula used:
V=IR
P=VI
∑V=0
Complete step-by-step answer:
We will first find out the maximum current that can travel in the circuit from the power rating of the diode and from the current get the voltage drop across the resistor and finally apply Kirchhoff’s voltage law for the loop to get the value of the resistance.
The power P consumed by an electrical device across which the voltage drop is V and the current through it being I is given by
P=VI --(1)
Also, the voltage drop V across a resistor of resistance R is given by
V=IR --(2)
where I is the current through the resistor.
According to Kirchhoff’s voltage law, the algebraic sum of the potential drops V through a complete closed loop is equal to zero.
∑V=0 --(3)
Now, let us analyze the question.
Since the total circuit has a single branch, there is only one current that flows through all the elements. Let this current be I.
The voltage drop across the diode remains constant at all currents. It is equal to Vdiode=0.6V.
The voltage of the cell is Vcell=1.6V.
Let the voltage drop across the resistor drop be VR.
The power rating of the diode is Pdiode=300mW=0.3W (∵1mW=0.001W)
Now, using (1), we get
0.3=0.6×I
∴I=0.60.3=0.5A --(4)
Hence, the current in the circuit is 0.5A.
Now, using (2), we get
VR=IR --(5)
Putting (4) in (5), we get
VR=0.5R --(6)
Now, we will apply Kirchhoff’s voltage law for the complete loop. We traverse the loop in a clockwise manner and according to convention the voltage gains are positive while the voltage drops are negative. Therefore, using (3), we get
Vcell−VR−Vdiode=0
∴1.6−VR−0.6=0
∴1.6−0.6=VR
∴VR=1V --(7)
Putting (7) in (6), we get
1=0.5R
R=0.51=2Ω
Therefore, the required value of the resistance is 2Ω.
Therefore, the correct option is B) 2Ω.
So, the correct answer is “Option B”.
Note: We could have also solved this problem by calculating the power consumed by the resistor from the values of the current and the resistance (PR=I2R). Then, keeping in accordance with the principle of conservation of energy, the sum of the powers consumed by the resistor and the diode would have been equal to the power supplied by the cell (Pcell=VcellI). From this we would have got the value of the power consumed by the resistor and from which we would have got the value of the resistance.
