Question

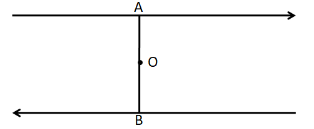
The diagram shows two antiparallel currents that are equal in magnitude. AB is a line perpendicular to both the currents and O is its center. Consider now the following statements
(i) The resultant magnetic field at O is non-zero.
(ii) The magnitude of the magnetic field along AB is constant.
(iii) The direction of the magnetic field is the same everywhere on AB.
Which of the following is correct?

(A) (i), (ii) and (iii)
(B) (i) and (ii)
(C) (i) and (iii)
(D) (ii) and (iii)

Answer 1

To solve this question, we need to use the ampere’s circuital law in order to determine the magnitude of the electric field between the currents. For finding out the direction of the magnetic field, we can use the right hand rule.

Formula used: The formula which is used in solving this question is given by
$B = \dfrac{{{\mu _0}I}}{{2\pi r}}$, here $B$ is the magnetic field produced by a straight current carrying conductor at a perpendicular distance of $r$ from it.

Complete step by step solution:
Let the distance between the two currents be $d$ and the magnitude of the current be $I$. Now, let us consider a point C on the line AB, at a distance of $x$ from the upper current, as shown in the figure below.

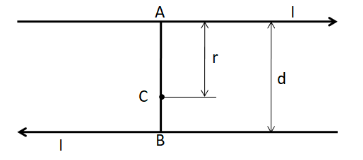
The magnetic field due to the upper current at C is given by
${B_1} = \dfrac{{{\mu _0}I}}{{2\pi r}}$ (1)
Also, the magnetic field due to the lower current at C is
${B_2} = \dfrac{{{\mu _0}I}}{{2\pi \left( {d - r} \right)}}$ (2)
By the right hand thumb rule, we get the direction of both ${B_1}$ and ${B_2}$to be into the plane of the paper. Therefore the total magnetic field at C is
$B = {B_1} + {B_2}$
From (1) and (2)
$B = \dfrac{{{\mu _0}I}}{{2\pi r}} + \dfrac{{{\mu _0}I}}{{2\pi \left( {d - r} \right)}}$
$B = \dfrac{{{\mu _0}I}}{{2\pi }}\left( {\dfrac{1}{r} + \dfrac{1}{{\left( {d - r} \right)}}} \right)$
On simplifying, we get
$B = \dfrac{{{\mu _0}I}}{{2\pi }}\left( {\dfrac{{r + \left( {d - r} \right)}}{{r\left( {d - r} \right)}}} \right)$
$B = \dfrac{{{\mu _0}Id}}{{2\pi r\left( {d - r} \right)}}$ (3)
So as we can see that the magnetic field between A and B is dependent on the distance $r$. Therefore it is not constant along AB.
Thus the statement (ii) is incorrect.
Also, this magnetic field is into the plane of the paper, regardless of the distance $r$. So, its direction is the same everywhere on AB.
So the statement (iii) is correct.
Now, as the point O lies at the centre of the line AB, we have $r = d/2$ for this point.
Substituting $r = d/2$ in (3) we get the magnetic field at O as
$B = \dfrac{{{\mu _0}Id}}{{2\pi \left( {d/2} \right)\left( {d - d/2} \right)}}$
On simplifying we get
$B = \dfrac{{2{\mu _0}I}}{{\pi d}}$
So the magnetic field at O is clearly non-zero.
So the statement (i) is correct.
Thus, the correct statements are (i) and (iii).
Hence, the correct answer is option C.

Note:
We can attempt this question without even calculating the magnitude of the magnetic field. As the magnetic field produced by both the currents is in the same direction, so just with the help of the right hand thumb rule we can answer this question.