Question

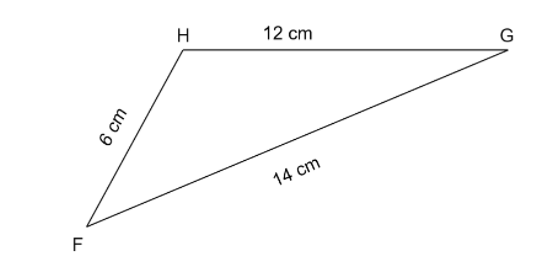
The diagram shows triangle $FGH$ , with $FG = 14{\text{ }}cm$ , $GH = 12{\text{ }}cm$ and $FH = 6{\text{ }}cm$ . Calculate the size of angle $HFG$.

Answer 1

Hint : We have to find the value of the angle $HFG$ . We solve this question using the concept of cosine law of trigonometry and using the values of trigonometric functions . We can find the values of angles of the triangle by applying cosine law . And thereafter finding the value of angle $HFG$ by putting the values in the formula of cosine law .

Complete step-by-step answer :
All the trigonometric functions are classified into two categories or types as either sine function or cosine function . All the functions which lie in the category of sine functions are sin , cosec and tan functions on the other hand the functions which lie in the category of cosine functions are cos , sec and cot functions . The trigonometric functions are classified into these two categories on the basis of their property which is stated as : when the value of angle is substituted by the negative value of the angle then we get the negative value for the functions in the sine family and a positive value for the functions in the cosine family .
Given :
$FG = 14{\text{ }}cm$ , $GH = 12{\text{ }}cm$ and $FH = 6{\text{ }}cm$
Let the angles be stated as $angle{\text{ }}F = angle{\text{ }}HFG$ , $angle{\text{ }}H = angle{\text{ }}FHG$ and $angle{\text{ }}G = angle{\text{ }}HGF$ .
We know ,
Formula of cosine law is given as :
$\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}$
Now , after putting the values we will get the value for $angle{\text{ }}C$
Putting the values for the formula , we get
$\cos F = \dfrac{{{{(FH)}^2} + {{(FG)}^2} - {{(HG)}^2}}}{{2 \times FH \times FG}}$
Putting the values in the formula , we get
After solving we get ,
$\cos F = \dfrac{{{6^2} + {{14}^2} - {{12}^2}}}{{2 \times 6 \times 14}}$
On further simplifying , we get
$\cos F = \dfrac{{36 + 196 - 144}}{{2 \times 6 \times 14}}$
We get ,
$\cos F = \dfrac{{88}}{{168}}$
After further simplifying , we get
$\cos F = \dfrac{{11}}{{21}}$
Taking ${\cos ^{ - 1}}$ both sides , we get
As , ${\cos ^{ - 1}}[\cos x] = x$
Then ,
$F = {\cos ^{ - 1}}\left[ {\dfrac{{11}}{{21}}} \right]$
Thus the value of angle $HFG$ is $F = {\cos ^{ - 1}}\left[ {\dfrac{{11}}{{21}}} \right]$ .
So, the correct answer is “$F = {\cos ^{ - 1}}\left[ {\dfrac{{11}}{{21}}} \right]$”.

Note : The formula of triangle law of sine is given as :
$\dfrac{a}{{\sin A}} = \dfrac{b}{{\sin B}} = \dfrac{c}{{\sin C}}$
The formula of triangle law of cosine is given as :
$\cos A = \dfrac{{{b^2} + {c^2} - {a^2}}}{{2bc}}$
Where $A$ , $B$ , $C$ are the angles of the triangle $ABC$ and $a$ , $b$ , $c$ are the sides of the triangle $ABC$.
These formulas must be remembered. Calculations must be verified to be sure of the answer.