Question

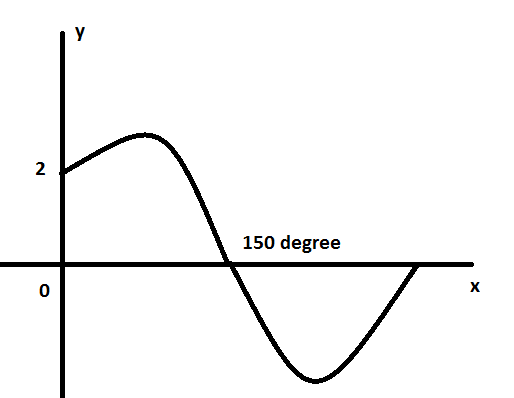
The diagram shows part of the graph of $y=k\sin (\theta +\alpha )$ , where k and $\alpha$ are constants and
$\left( {{0}^{\circ }}<\alpha <{{180}^{\circ }} \right)$. Find the value of $\alpha$ and the value of k.

Answer 1

Hint: In such questions where graph is involved and an equation of the graph is also given, we can simply plug in the coordinates from the graph and then find the values of the unknowns that are present in the equation.
In this question particularly, we can see where the graph is becoming zero and at that value of input, we can equate the expression with the already known output.

Complete step-by-step answer:
As mentioned in the question, we have to find the values of the unknowns that are there in the given equation.
Now, we will put the values by looking at the graph and then find the values of the variables as mentioned in the hint.
On putting the values into the equation, we get the following result
$2=k\sin (\alpha )\ \ \ \ \ ...(a)$
$0=k\sin ({{150}^{\circ }}+\alpha )\ \ \ \ \ ...(b)$
By observing the equation (a) and (b), we can say that

& \sin ({{150}^{\circ }}+\alpha )=0 \\\ & {{150}^{\circ }}+\alpha =0\ or\ {{180}^{\circ }}\ or\ {{360}^{\circ }} \\\ & \alpha =-{{150}^{\circ }}\ or\ {{30}^{\circ }}\ or\ {{210}^{\circ }} \\\ \end{aligned}$$ But as the value of $$\alpha $$ is given to be as $$\left( {{0}^{\circ }}<\alpha <{{180}^{\circ }} \right)$$ , hence, the value of $$\alpha $$ is $${{30}^{\circ }}$$ . Now, as the value of $$\alpha $$ is $${{30}^{\circ }}$$, so we can write as follows $$\begin{aligned} & 2=k\sin ({{30}^{\circ }}) \\\ & 2=\dfrac{k}{2} \\\ & k=4 \\\ \end{aligned}$$ Hence, the value of k is 4. NOTE: -The students can make an error if they don’t know how to read a graph as without knowing how to read a graph one could not get to the correct answer. Also, knowing the values of sin function for different values of the input is also very important to solve this question correctly.