Question
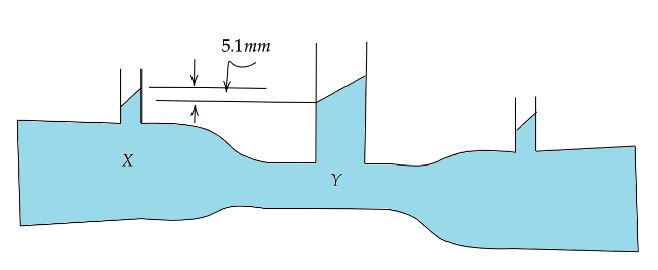
Question: The diagram shows a venturimeter through which water is flowing. The speed of water \(X\) is \(2\,cm...
The diagram shows a venturimeter through which water is flowing. The speed of water X is 2cms−1. The speed of water at Y ( taking g=10ms2 ) is
A. 23cms−1
B. 32cms−1
C. 101cms−1
D. 1024cms−1
Solution
Here we have to use the formula of the venturimeter. The formula shows the pressure difference between X that is before narrowing of the pipe and Y that is after narrowing of the pipe. After that using the pressure difference formula of fluid we can solve the equation to find the value of speed of water at Y.
Complete step by step answer:
As per the problem we have a venturimeter through which water is flowing. The speed of water X is 2cms−1. Now we need to calculate the speed of water at Y.
We know venture effect is represented as,
px−py=2ρ(vy2−vx2)……(1)
Where, Pressure at position X before the narrowing of the pipe is px, Pressure at position Y after the narrowing of the pipe is py, Density of fluid travelling in the pipe is ρ, Velocity of the fluid at position Y is vy and Velocity of the fluid at position X is vx.
The pressure difference is also represented as,
px−py=Δhρg……(2)
Where,
Δh is the change in height due to change in before and after narrowing of the pipe.
Now equation equation (1) and (2) we will get,
2ρ(vy2−vx2)=Δhρg
Now cancelling the common terms we will get,
21(vy2−vx2)=Δhg
We know,
Δh=5.1mm=0.51cm
⇒vx=2cms−1
⇒g=10ms−1=1000cms−1
Now putting the given values in the above equation we will get,
21(vy2−22)=0.51×1000
Now on rearranging and solving further solving we will get,
vy2=(510×2)+2=1024
Hence we can say the speed of water at Y is 32cms−1.
Therefore the correct option is (B).
Note: Here we converted all the units of length in centimeter as our option is given in centimeter. Remember that a venturimeter is a device which is used to measure the rate of flow of fluid flowing through a pipe. The principle of venturimeter is that when a fluid flows through it, it’s acceleration in the convergent section and decelerates in the divergent section which results in drop in static pressure.
