Question
Question: The diagram shows a uniformly charged hemisphere of radius R. It has volume charge density \(\rho \)...
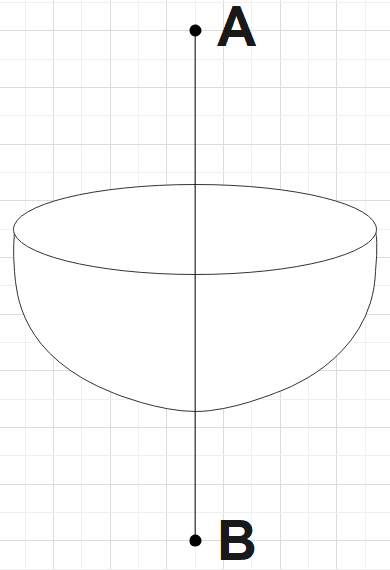
The diagram shows a uniformly charged hemisphere of radius R. It has volume charge density ρ. If the field at a point 2R distance above its centre is E then what is the electric field at the point which is 2R below its centre?
A. 6ε0ρR+E
B. 12ε0ρR−E
C. −6ε0ρR+E
D. 12ε0ρR+E
Solution
As a very first step, one could read the question well and hence understand the question. Then one could consider the whole sphere of which the given hemisphere forms the half of. After that apply simple logic to find the required electric field with the current knowledge of electric field E.
Complete answer:
In the question, we are given a diagram that shows a uniformly charged hemisphere that has a radius R and volume charge density of ρ. We are also told that the field at distance 2R above its centre is E and we are supposed to find the electric field at a point that is 2R below its centre.
As the points A and B are equidistant from each other and the centre of the sphere, on considering the whole sphere of which given hemisphere forms a part of, we could say that,
Electric field at the lower part at A is equal to the field due to the upper part at B.
Also,
Electric field at B due to the lower half = electric field due to the full sphere – electric field due to the upper half.
Electric field due to the whole sphere could be given by,
ES=(2R)2KQ=4R2ρ(34πR3)=12ε0ρR…………………………….. (1)
Electric field due to the given hemisphere at B would be,
EB=ES−E
Substituting (1),
∴EB=12ε0ρR−E
Therefore, we found the required field to be,
EB=12ε0ρR−E
Hence, option B is found to be the correct answer.
Note: Electric field can be defined as the physical field that is known to surround the electrically charged particles. And these fields also exert force on all other charged particles that are present in the field. This force exertion is done either by attracting or repelling them. Origin of these fields can be from electric charges or may be time varying magnetic fields.
