Question

The diagram shows a straight line KL. P is a point which moves so that it is equidistant from the point K and the point L. Which of the following is the locus of P?

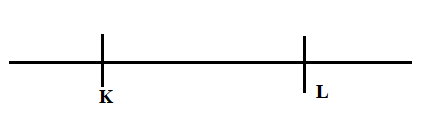
A.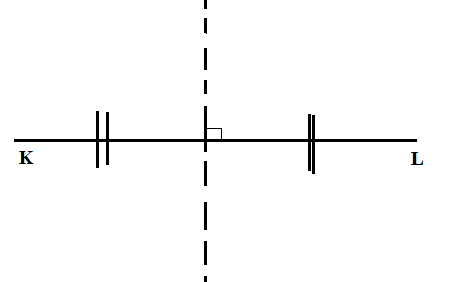
B.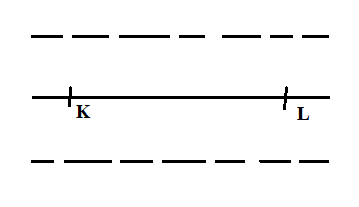
C.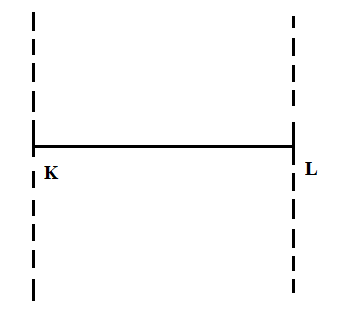
D.

Answer 1

Here, the point P moves such that P is at the same distance from point K and point L. We will begin by taking the midpoint of the line as origin and then apply distance formula and then observe the figure according to the derived condition.

Complete step-by-step answer:
We are given the line KL.
Let the midpoint of the given line be the origin.
We will assume the distance of KL as $2a$ units.
And let the coordinates of P be $\left( {x,y} \right)$
Then, the coordinates of K will be $\left( { - a,0} \right)$ and $\left( {a,0} \right)$
Since, the distance KP is equal to PL, we have
$\Rightarrow {\left( {x - \left( { - a} \right)} \right)^2} + {\left( {y - 0} \right)^2} = {\left( {a - x} \right)^2} + {\left( {0 - y} \right)^2} \\\ \Rightarrow {\left( {x + a} \right)^2} = {\left( {a - x} \right)^2} \\\$
Here, we can see that the $x = 0$ is the only solution of the above equation.
Then, the locus of P is the perpendicular bisector of KL.

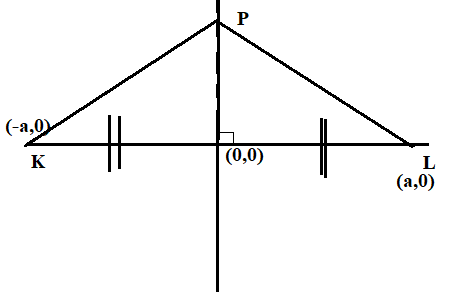
Hence, option A is correct.

Note: We have considered the KL on the $x$ axis. We can also solve this question by letting KL on the $y$ axis. The distance formula between points $\left( {{x_1},{y_1}} \right)$ and $\left( {{x_2},{y_2}} \right)$ is given as $\sqrt {{{\left( {{x_1} - {x_2}} \right)}^2} + {{\left( {{y_1} - {y_2}} \right)}^2}}$