Question
Question: The diagram shows a square-based pyramid with base lengths \[6\text{ }inch\] and height\[8\text{ }in...
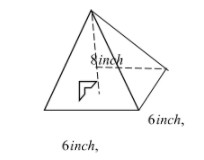
The diagram shows a square-based pyramid with base lengths 6 inch and height8 inch. What is the volume (in inch3) of the pyramid?
A) 64
B) 96
C) 144
D) 288
Solution
Separate the known and unknown terms and use the applicable equations for the required solution. So, here we will use the formula for volume of the pyramid =31 ×Area of base×height. For this first we need to find the area of the square base =side2.
Complete step-by-step solution
Given: The base length of the pyramid = 6 inch,
The height of the pyramid =8 inch.
As we know that, Volume of the pyramid =31 ×Area of base×height ........... (1)
Area of the square is =side2=62=36sqinch.
Substitute the known values in the equation (1) we get,
Volume =31 ×36×8 [simplify the equations]
=96 inch3
The required solution -
Therefore, the volume (in inch3) of the pyramid with base lengths 6 inch and height 8 inchis, V=96inch3
Hence, from the given multiple choices, the option B is the correct answer.
Note: In such types of problems where the required dimensions of the certain parts are given, always find the correlation among the required terms. Always remember all the properties and formulas for the pyramid. Check the units of the given parameters and the unit asked in the required answer. Also remember the conversion relation among the different units.
