Question

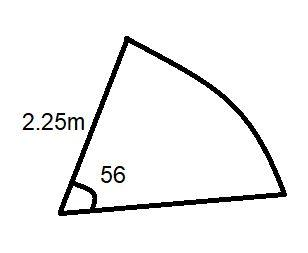
The diagram shows a sand pit in a child's play area. The shape of the sand pit is a sector of a circle of radius 2.25m and sector angle ${56^0}$ . Calculate the area of the sand pit.

Answer 1

Hint:-Here we use the formula of the area of the sector i.e. $\dfrac{\theta }{{{{360}^0}}} \times \pi {r^2}$. Because here in the figure the shape of the sand pit is in the shape of a sector of a circle.

Complete step-by-step answer:
Given radius of circle, r =2.25m by observing the given figure.
Arc subtends an angle of ${56^0}$ at center.
We know that for finding the area of the sector the formula we used is$\dfrac{\theta }{{{{360}^0}}} \times \pi {r^2}$.
Now we simply put the given values in the formula to find out the required area.
So the area of sector$= \dfrac{\theta }{{{{360}^0}}} \times \pi {r^2} = \dfrac{{56}}{{360}} \times \dfrac{{22}}{7} \times {(2.25)^2} = 2.474{m^2}$.
Therefore the required area of the sand pit is $2.474{m^2}$.

Note: - Whenever we face such a type of question we simply use the formula to get the answer. And if some time you forgot the formula you can apply a unitary method for solving the question. As you know the total angle at the center of the circle is ${360^0}$. And for that angle we know that the area of the circle is $\pi {r^2}$. Then for angle $\theta$ we apply a simply unitary method.