Question

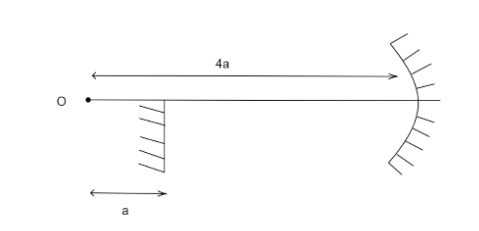
The diagram shows a mirror system. If after two reflections the image and the object O coincide with each other, then the value of the radius of curvature of the concave mirror is: (take $a = 3m$)

(A) $4m$
(B) $6m$
(C) $8m$
(D) $10m$

Answer 1

Hint The radius of the curvature of a mirror is twice of its focal length. Focal length can easily be calculated if the image and object position is given. For a plane mirror, the object distance is equal to image distance.

Step by step solution
Two conditions are given for this problem. First, the object is kept at O, i.e. a distance $4a$ from the concave mirror. Second, the final image after reflection from the plane mirror forms at O i.e. at a distance of $a$ behind the plane mirror.
Since object distance and image distance are always equal for a plane mirror, we can say that the object for the plane mirror is placed at position $P$

Using the given condition that reflection takes place twice, we can conclude that first, it reflects from the concave mirror and then from the plane mirror to make the final image at O. This implies that the object for the plane mirror is actually the image from the concave mirror.
So, we have the object distance and image distance for the concave mirror.
$u = - 4a$
And, $v = - 2a$.
Where, $u$ object distance
$v$ is the image distance.
The negative sign represents that these coordinates are on the left side of the pole of the mirror.
Using mirror formula,
$\dfrac{1}{v} + \dfrac{1}{u} = \dfrac{1}{f}$
Putting the values, we get
$\dfrac{1}{{ - 2a}} + \dfrac{1}{{ - 4a}} = \dfrac{1}{f}$
$\Rightarrow \dfrac{{ - 2 - 1}}{{4a}} = \dfrac{1}{f}$
Solving this
$\dfrac{1}{f} = \dfrac{{ - 3}}{{4a}}$
We know that, radius of curvature of a mirror is given by twice its focal length.
$R = 2f$
$\Rightarrow R = 2\left( {\dfrac{{ - 4a}}{3}} \right)$
Putting $a = 3m$, we get
$R = 8m$.

Hence, Option (C) is correct.

Note The basic concept is to remember the mirror formulas. You should be careful if you are taking the numeric value of the image and object distance because it can easily lead you to error. A better way is to solve it first and then put the numeric value.