Question

The diagram represents the plane (top view) of a cubical room, with the wall CD as a plane mirror. Each side of the room will be $3m$in length. A camera P has been kept at the midpoint of the wall AB. At what distance must the camera be focused in order to photograph the image of a body kept at A?

Answer 1

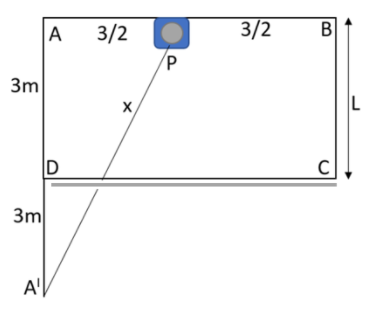
It has been mentioned in the question that the location of the image of the body placed at point A will be $3m$ below the plane mirror. Hence the camera must be focussed at a distance will be equivalent to distance $P{A}'$. The distance $P{A}'$ can be found by taking the square root of the sum of the square of the altitude of the right triangle we are considering and the square of the base of the right triangle. Substitute the values in this equation. This will help you in answering this question.

Complete answer:
It has been mentioned in the question that the location of the image of the body placed at point A will be $3m$ below the plane mirror. Hence the camera must be focussed at a distance will be equivalent to distance $P{A}'$. The distance $P{A}'$ can be found by taking the square root of the sum of the square of the altitude of the right triangle we are considering and the square of the base of the right triangle.
This can be written as an equation given as,
$x=\sqrt{A{{{{A}'}}^{2}}+P{{A}^{2}}}$
Let us consider the right triangle $\Delta PA{A}'$now.
The altitude of this triangle can be shown as,
$A{A}'=3+3=6m$
The base of this right triangle can be written as,
$PA=\dfrac{3}{2}m$
Substituting the values in this equation can be shown as,
$x=\sqrt{{{6}^{2}}+{{\dfrac{3}{2}}^{2}}}=6.18m$
Hence the distance must the camera be focused in order to photograph the image of a body kept at A has been found. The correct answer has been obtained.

Note:
The Pythagorean Theorem which can be otherwise referred to as Pythagoras's theorem. This can be defined as a fundamental equation in Euclidean geometry among the three sides of a right triangle. This equation says that the area of the square whose side is the hypotenuse will be equivalent to the sum of the areas of the squares on the other two sides.