Question
Question: The diagram below shows a modified meter bridge which is used for measuring two unknown resistances ...
The diagram below shows a modified meter bridge which is used for measuring two unknown resistances at the same time. The first galvanometer gives the balance point at C and the second one fives the balance point at D. Using the details given in the diagram, find out the values of R1 andR2 [This question may have multiple correct options].
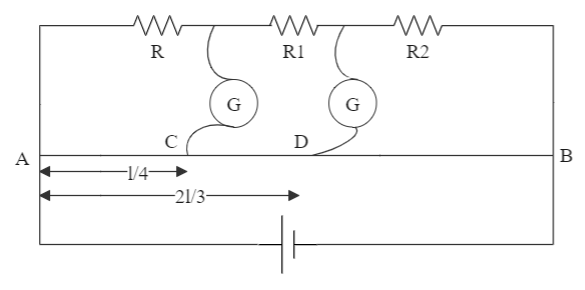
(A) R1=35R
(B) R2=34R
(C) R1=34R
(D) R2=35R
Solution
When a meter bridge is balanced at a certain point, it is used to find the unknown resistances in its setup. In this question, the two galvanometers work independently. So, the two unknown resistances can be found by solving linear equations made with the help of balance.
Formula used: R2R1=total−ll where R1 and R2 are two resistances on either side of the galvanometer jockey, l is the length at which the jockey is touched on the scale and total is the full length of the meter scale.
Complete step by step answer:
In a meter bridge, the galvanometer is connected between the resistances to the wire using a jockey. As the jockey touches the taut wire at some point, an electrical connection is established that renders a balance between the total resistance per unit length on both sides of the point.
In this question, the galvanometer touches two points and we are asked to find two unknown resistances. Let us first calculate the distances AC, CB and AD, DB so that the two sides can be easily balanced.
AC=4l
CB=l−4l=43l
AD=32l
DB=l−32l=3l
Now, using the balance equation at point C we try to find the values of unknown resistances as:
R1+R2R=CBAC
Putting the values of AC and CB, we get:
R1+R2R=43l4l
⇒R1+R2R=31 [By dividing and cancelling l]
Cross-multiplying and rearranging the two gives us:
