Question

The diagonals of the parallelogram whose sides are $lx+my+n=0$ , $lx+my+n'=0$ , $mx+ly+n=0$ , $mx+ly+n'=0$ include an angle:
1)$\dfrac{\pi }{2}$
2) $\dfrac{\pi }{4}$
3) $\dfrac{\pi }{3}$
4) None of these

Answer 1

Here in this question we have been asked to find the angle between the diagonals of the parallelogram whose sides are $lx+my+n=0$ , $lx+my+n'=0$ , $mx+ly+n=0$ , $mx+ly+n'=0$ . For answering this question we will conclude the type of parallelogram is rectangle, square or rhombus.

Complete step-by-step solution:
Now considering from the question we have been asked to find the angle between the diagonals of the parallelogram whose sides are $lx+my+n=0$ , $lx+my+n'=0$ , $mx+ly+n=0$ , $mx+ly+n'=0$ .
Now we will find the type of parallelogram it is rectangle, square or rhombus.
We know that in a rhombus the length of all sides is equal and the angle between the diagonals is a right angle. The angle between the adjacent sides is not a right angle.

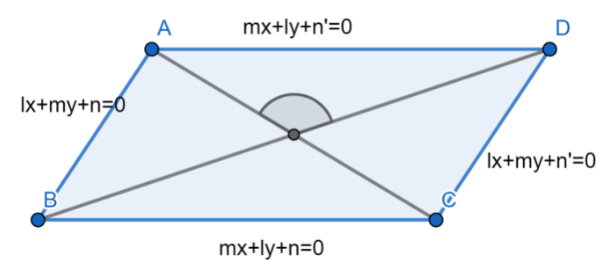
We know that the slope of the line $ax+by+c=0$ is $\dfrac{-a}{b}$ .
From the basic concepts we know that the distance between two parallel lines $ax+by+c=0$ and $ax+by+c'=0$ is given as $\dfrac{\left| c-c' \right|}{\sqrt{{{a}^{2}}+{{b}^{2}}}}$ .
Hence the distance between the opposite sides in the given parallelogram is $\dfrac{\left| n-n' \right|}{\sqrt{{{l}^{2}}+{{m}^{2}}}}$ .
The product of slopes of the adjacent will be $\dfrac{-l}{m}\times \dfrac{-m}{l}=1$ .
Therefore we can conclude that the given parallelogram is rhombus so the angle between the diagonals is $\dfrac{\pi }{2}$ .
Hence we will mark the option “1” as correct.

Note: We know that in a square the length of all sides is equal and the angle between the diagonals is a right angle and the angle between the adjacent sides is a right angle. We know that in a rectangle the length of all sides is not equal and the angle between the diagonals is not a right angle and the angle between the adjacent sides is a right angle.