Question
Question: The diagonals of a rhombus are 12cm and 7.5cm. Find its area....
The diagonals of a rhombus are 12cm and 7.5cm. Find its area.
Solution
Hint: Use the fact that the diagonals of a rhombus bisect each other at right angles. Using the property that the area of a triangle with base b and height h is given by 21bh. Hence find the area of each of the triangles in which the rhombus is divided by the diagonals. Hence find the area of the rhombus. Alternatively, use the fact that the area of the rhombus with diagonals d1 and d2 is given by 21d1d2. Hence determine the area of the rhombus.
Complete step-by-step answer:
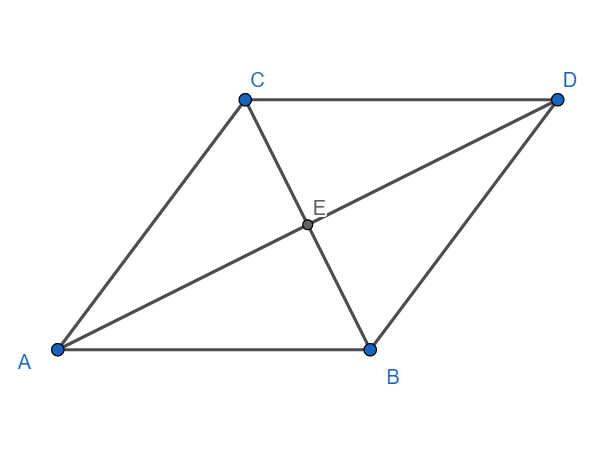
Consider the rhombus ABCD, with AD = 12cm and BC = 7.5cm.
Since the diagonals of a rhombus bisect each other, we have
CE=27.5=3.75=BE and AE=212=6=DE.
Now, we have
In the triangle DEC DE⊥CE(diagonals of a rhombus are perpendicular to each other).
Hence, we have
ar(ΔDEC)=21×DE×CE=21×6×3.75=11.25
Similarly, we have
ar(ΔBEC)=ar(ΔAEB)=ar(ΔAEC)=11.25
The area of the rhombus ABCD is the sum of the area of the triangle AEB, AEC, DEC and DEB
Hence, we have
ar(ABCD)=11.25+11.25+11.25+11.25=4×11.25=45
Hence the area of the rhombus ABCD = 45 square centimetres.
Note: Alternatively, we know that the area of a rhombus with diagonals d1 and d2 is given by 21d1d2
Here, we have
d1=12cm and d2=7.5cm
Hence, the area of rhombus
=21(12)×(7.5)=45 square centimetres, which is the same as obtained above.
