Question

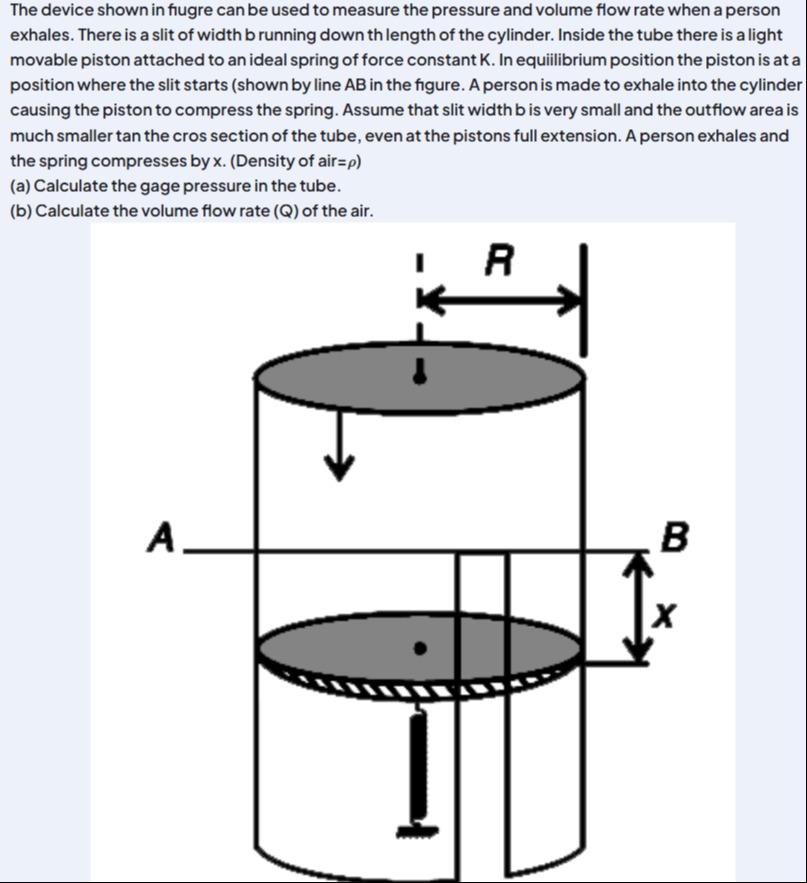
The device shown in flugre can be used to measure the pressure and volume flow rate when a person exhales. There is a slit of width b running down th length of the cylinder. Inside the tube there is a light movable piston attached to an ideal spring of force constant K. In equiilibrium position the piston is at a position where the slit starts (shown by line AB in the figure. A person is made to exhale into the cylinder causing the piston to compress the spring. Assume that slit width b is very small and the outflow area is much smaller tan the cros section of the tube, even at the pistons full extension. A person exhales and the spring compresses by x. (Density of air=$\rho$) (a) Calculate the gage pressure in the tube. (b) Calculate the volume flow rate (Q) of the air.

Answer 1

(a) The gage pressure in the tube is: $P_{gage} = \frac{Kx}{\pi R^2}$

(b) The volume flow rate (Q) of the air is: $Q = bx \sqrt{\frac{2Kx}{\rho \pi R^2}}$

Answer 2

The problem describes a device to measure pressure and volume flow rate of exhaled air. A piston connected to a spring is pushed by the exhaled air, compressing the spring by a distance $x$. Air then exits through a slit whose open area depends on $x$.

Part (a): Calculate the gage pressure in the tube.

1. Identify forces on the piston:

   • The air inside the tube exerts a downward force on the piston: $F_{in} = P_{in} A$, where $P_{in}$ is the pressure inside the tube and $A$ is the cross-sectional area of the piston.
   • The atmospheric pressure outside exerts an upward force on the piston: $F_{atm} = P_{atm} A$.
   • The spring, compressed by $x$, exerts an upward force: $F_s = Kx$, where $K$ is the spring constant.

2. Apply equilibrium condition:

   When the piston is in equilibrium at compression $x$, the net force on it is zero. Assuming the piston is light, we can ignore its weight. $F_{in} = F_{atm} + F_s$ $P_{in} A = P_{atm} A + Kx$

3. Define gage pressure:

   Gage pressure ($P_{gage}$) is the pressure inside the tube relative to the atmospheric pressure outside: $P_{gage} = P_{in} - P_{atm}$.

4. Substitute and solve for gage pressure:

   $(P_{in} - P_{atm}) A = Kx$ $P_{gage} A = Kx$ The cross-sectional area of the piston is $A = \pi R^2$, where $R$ is the radius of the cylinder. $P_{gage} (\pi R^2) = Kx$ $P_{gage} = \frac{Kx}{\pi R^2}$

Part (b): Calculate the volume flow rate (Q) of the air.

1. Apply Bernoulli's Principle:

   Consider the flow of air from inside the tube (point 1) to outside the slit (point 2). Bernoulli's equation states: $P_1 + \frac{1}{2}\rho v_1^2 + \rho g h_1 = P_2 + \frac{1}{2}\rho v_2^2 + \rho g h_2$.

   • Let $P_1 = P_{in}$ and $v_1$ be the velocity of air inside the tube.
   • Let $P_2 = P_{atm}$ and $v_2$ be the velocity of air exiting the slit.
   • Since the flow is horizontal, we can neglect height differences: $h_1 \approx h_2$.

   The equation simplifies to: $P_{in} + \frac{1}{2}\rho v_1^2 = P_{atm} + \frac{1}{2}\rho v_2^2$.

2. Apply Continuity Equation and simplify:

   The problem states that "the outflow area is much smaller than the cross section of the tube". Let $A_{tube}$ be the cross-sectional area of the tube ($A_{tube} = \pi R^2$). The outflow area of the slit is $A_{slit} = b \times x$, where $b$ is the width of the slit and $x$ is its length (equal to the spring compression). Continuity equation: $A_{tube} v_1 = A_{slit} v_2$. Since $A_{slit} \ll A_{tube}$, it implies that $v_1 \ll v_2$. Therefore, we can approximate $v_1 \approx 0$.

3. Solve for exit velocity ($v_2$):

   With $v_1 \approx 0$, Bernoulli's equation becomes: $P_{in} = P_{atm} + \frac{1}{2}\rho v_2^2$ $P_{in} - P_{atm} = \frac{1}{2}\rho v_2^2$ Since $P_{in} - P_{atm} = P_{gage}$, we have: $P_{gage} = \frac{1}{2}\rho v_2^2$ Substitute the expression for $P_{gage}$ from part (a): $\frac{Kx}{\pi R^2} = \frac{1}{2}\rho v_2^2$ $v_2^2 = \frac{2Kx}{\rho \pi R^2}$ $v_2 = \sqrt{\frac{2Kx}{\rho \pi R^2}}$

4. Calculate Volume Flow Rate (Q):

   The volume flow rate is the product of the outflow area and the exit velocity: $Q = A_{slit} \times v_2$ $Q = (bx) \times \sqrt{\frac{2Kx}{\rho \pi R^2}}$ $Q = bx \sqrt{\frac{2Kx}{\rho \pi R^2}}$

Explanation of the solution:

(a) Gage pressure is found by balancing the force exerted by the pressure difference on the piston with the spring's restoring force ($F=Kx$). The pressure difference is $P_{gage} = P_{in} - P_{atm}$. The force on the piston due to this pressure difference is $P_{gage} \times (\text{piston area})$. Equating this to $Kx$ gives $P_{gage} = \frac{Kx}{\pi R^2}$.

(b) Volume flow rate is calculated using Bernoulli's principle and the continuity equation. Due to the small outflow area compared to the tube's cross-section, the air velocity inside the tube is negligible. Bernoulli's principle then simplifies to $P_{gage} = \frac{1}{2}\rho v_{exit}^2$, allowing calculation of the exit velocity $v_{exit}$. The volume flow rate $Q$ is then $A_{slit} \times v_{exit}$, where $A_{slit} = bx$.