Question
Question: The determinant $\begin{vmatrix} ^{x}C_1 & ^{x}C_2 & ^{x}C_3 \\ ^{y}C_1 & ^{y}C_2 & ^{y}C_3 \\ ^{z}C...
The determinant xC1yC1zC1xC2yC2zC2xC3yC3zC3
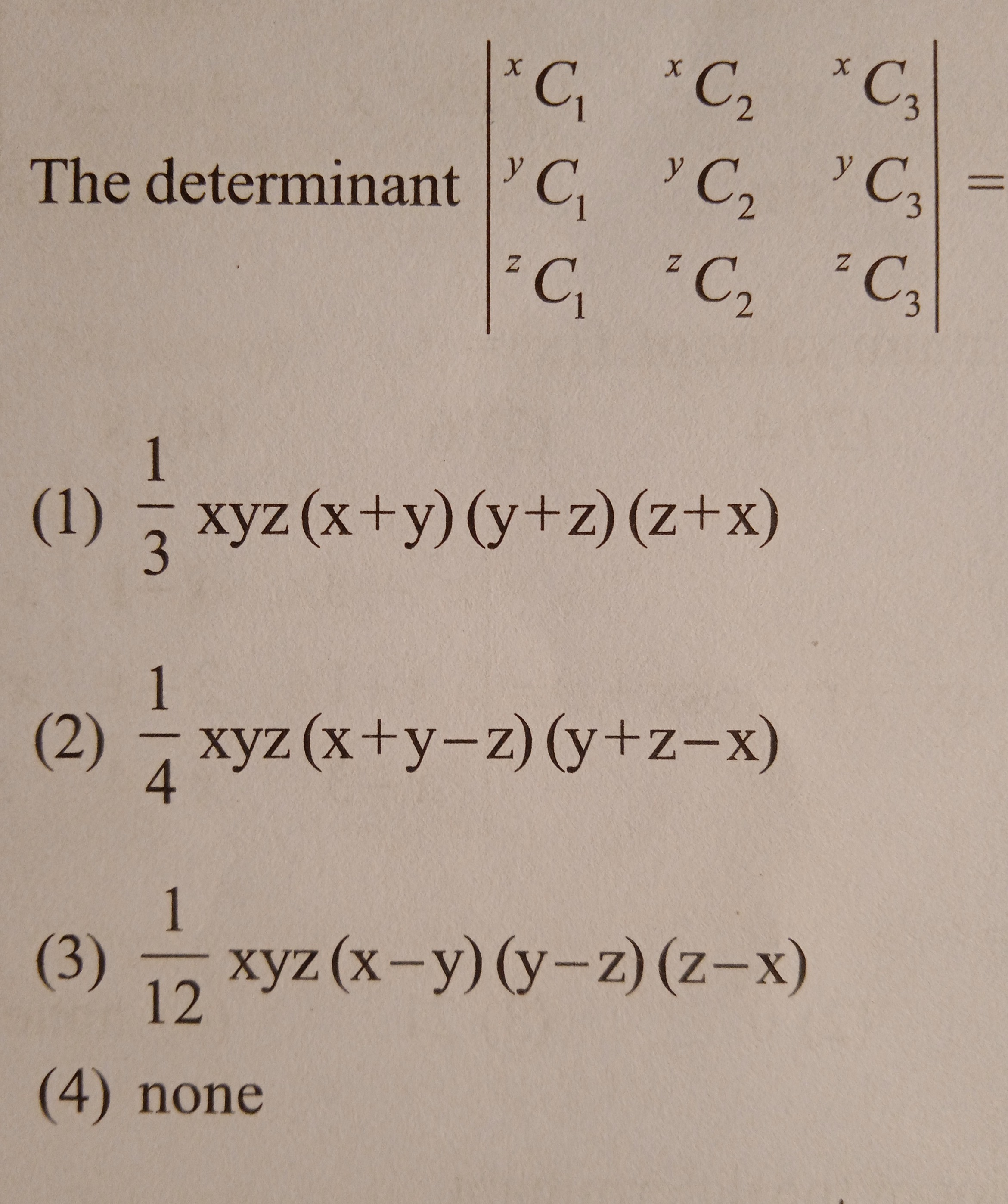
A
31xyz(x+y)(y+z)(z+x)
B
41xyz(x+y-z)(y+z-x)
C
121xyz(x-y)(y-z)(z-x)
D
none
Answer
121xyz(x−y)(y−z)(z−x)
Explanation
Solution
The given determinant is
xC1yC1zC1xC2yC2zC2xC3yC3zC3Recall that
nC1=n,nC2=2n(n−1),nC3=6n(n−1)(n−2).Thus, the matrix becomes
xyz2x(x−1)2y(y−1)2z(z−1)6x(x−1)(x−2)6y(y−1)(y−2)6z(z−1)(z−2).Step 1. Factor out x, y, z from rows 1, 2, 3 respectively:
=xyz⋅1112x−12y−12z−16(x−1)(x−2)6(y−1)(y−2)6(z−1)(z−2).Step 2. Factor out constants from columns 2 and 3: factor 21 from column 2 and 61 from column 3. The overall factor becomes 21⋅61=121:
=12xyz⋅111x−1y−1z−1(x−1)(x−2)(y−1)(y−2)(z−1)(z−2).Step 3. Substitute u=x−1,v=y−1,w=z−1. Then the determinant becomes
D=12xyz⋅111uvwu(u+1)v(v+1)w(w+1).Subtract the first row from the others:
R2→R2−R1,R3→R3−R1,yielding
D=12xyz⋅100uv−uw−uu(u+1)v(v+1)−u(u+1)w(w+1)−u(u+1).Note that
v(v+1)−u(u+1)=(v2+v)−(u2+u)=(v−u)(v+u+1), w(w+1)−u(u+1)=(w−u)(w+u+1).Thus, the 2×2 determinant becomes
(v−u)(w−u)[(w+u+1)−(v+u+1)]=(v−u)(w−u)(w−v).Returning to original variables:
v−u=(y−1)−(x−1)=y−x,w−u=z−x,w−v=z−y.So,
D=12xyz(y−x)(z−x)(z−y).Observe that
(y−x)(z−x)(z−y)=(x−y)(y−z)(z−x)(up to rearrangement of factors, which does not change the product since the number of sign changes is even).
Final Answer:
121xyz(x−y)(y−z)(z−x)