Question
Question: The descending pulley shown in figure has a radius 20 cm and moment of inertia \(0.20kg - {m^2}\). T...
The descending pulley shown in figure has a radius 20 cm and moment of inertia 0.20kg−m2. The fixed pulley is light and the horizontal plane frictionless. Find the acceleration of the block if its mass is 1.0 kg.
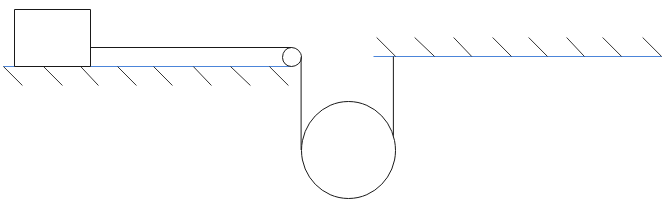
Solution
The block is connected to one string. The pulley is connected to two strings. The pulley is having some weight. So it will have both linear acceleration and angular acceleration. The tensions in both strings connecting two pulleys will be different and we will find out using the torque equation.
Formula used:
τ=Iα
Complete answer:
Since t5wo strings are connected to pulley and only one string is connected to the block, their acceleration will be different but interdependent.
If pulley moves ‘x’ distance down, then the block moves ‘2x’ distance right. So if acceleration of the block is ‘a’ then acceleration of the pulley will be ‘a/2’. If we refer the diagram below we have
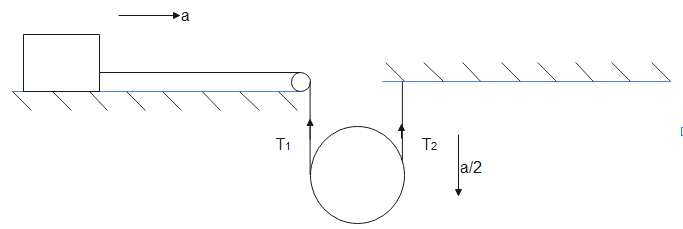
Tension of string connecting block is T1. Let the mass of the block is ‘m’ and pulley is ‘M’. For block we have
\eqalign{
& {T_1} = ma \cr
& \Rightarrow {T_1} = \left( 1 \right)a \cr
& \therefore {T_1} = a \cr}
Acceleration of pulley be ap which is equal to a/2.
We have
\eqalign{
& {a_p} = r\alpha \cr
& \tau = I\alpha \cr}
Where α is the angular acceleration of pulley and ‘I’ is moment of inertia of pulley and ‘r’ is the radius of pulley and τ is the torque acting on pulley.
\eqalign{
& \tau = \left( {{T_2} - {T_1}} \right)r \cr
& \Rightarrow r = 20cm = 0.2m \cr
& \Rightarrow \left( {{T_2} - {T_1}} \right)r = I\alpha \cr
& \Rightarrow \left( {{T_2} - {T_1}} \right)\left( {0.2} \right) = \left( {0.2} \right)\alpha \cr
& \Rightarrow \left( {{T_2} - {T_1}} \right) = \alpha \cr
& \Rightarrow {a_p} = r\alpha \cr
& \Rightarrow {a_p} = 0.2\alpha \cr
& \Rightarrow \dfrac{a}{2} = 0.2\alpha \cr
& \Rightarrow \alpha = 2.5a \cr
& \therefore \left( {{T_1} - {T_2}} \right) = - 2.5a \cr}
We have got angular acceleration in terms of ‘a’ and difference in tensions in terms of ‘a’. Now we will apply Newton's second law for the pulley.
\eqalign{
& I = \dfrac{{M{r^2}}}{2} \cr
& \Rightarrow M = \dfrac{{2 \times 0.2}}{{{{\left( {0.2} \right)}^2}}} \cr
& \Rightarrow M = 10kg \cr
& \Rightarrow Mg - \left( {{T_1} + {T_2}} \right) = M{a_p} = M\dfrac{a}{2} \cr
& \Rightarrow {T_1} - {T_2} = - 2.5a \cr
& \Rightarrow {T_1} = a \cr
& \Rightarrow 9.5a = Mg \cr
& \therefore a = \dfrac{{10 \times 9.8}}{{9.5}} = 10.315m/{s^2} \cr}
Hence acceleration of pulley will be 10.315 meter per second square.
Note:
If pulley is massless, then the moment of inertia of pulley will be zero. When it is zero then the difference in two tensions of strings will be zero and that means tension will be the same in two strings connecting the pulley. If pulley is having friction then the case would be different and methodology would be different.
