Question
Question: The derivative of $Y = \log_{10}^{x} + \log_{x}^{10} + \log_{x}^{8} + \log_{10}^{10}$...
The derivative of Y=log10x+logx10+logx8+log1010
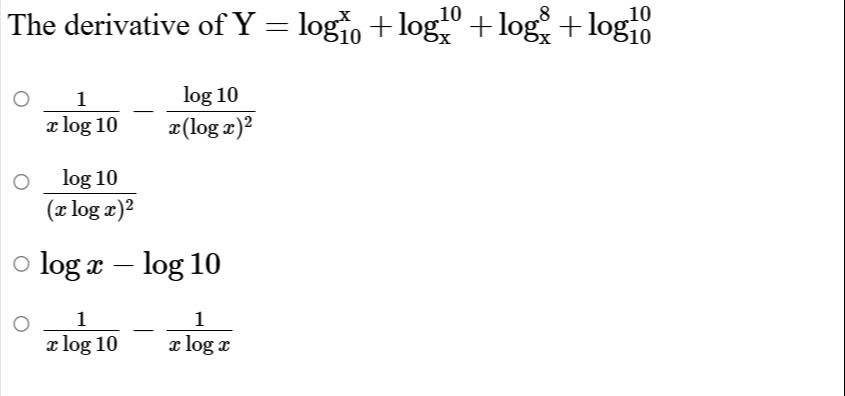
xlog101−x(logx)2log10
(xlogx)2log10
logx−log10
xlog101−xlogx1
xlog101−x(logx)2log10
Solution
The derivative of Y=log10x+logx10+log108+log1010 is calculated.
Using the change of base formula for logarithms, logba=lnblna: Y=ln10lnx+lnxln10+ln10ln8+ln10ln10 Y=ln101lnx+ln10(lnx)−1+ln10ln8+1
Differentiating term by term with respect to x:
- dxd(ln101lnx)=ln101⋅x1=xln101
- dxd(ln10(lnx)−1)=ln10⋅(−1)(lnx)−2⋅x1=−x(lnx)2ln10
- dxd(ln10ln8)=0 (since it's a constant)
- dxd(1)=0 (since it's a constant)
Combining these terms, the derivative is: dxdY=xln101−x(lnx)2ln10
Assuming that log in the options refers to the natural logarithm (ln), this result exactly matches the first option. This suggests that the original question notation log10x was intended as log10x, and logx8 and log1010 were intended as constants log108 and log1010 respectively, or that the terms with base 'x' were meant to be constants. The interpretation that yields a matching option is:
Y=log10x+logx10+(constants)
