Question

The depression in freezing point of 0.01 molal aqueous CH3COOH solution is 0.02046°C. 1 molal urea solution freezes at -1.86°C. Assuming molality is equal to molarity, pH of the solution would be

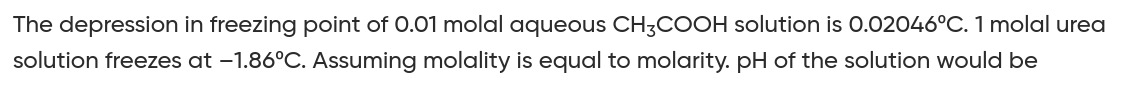
• A. 2
• B. 3
• C. 4
• D. 5

Answer 1

Answer: (B)

3

Answer 2

1. Calculate the cryoscopic constant ($K_f$) for water:

Urea is a non-electrolyte, so its van't Hoff factor ($i$) is 1. The freezing point depression for a 1 molal urea solution is $\Delta T_f = 0^\circ C - (-1.86^\circ C) = 1.86^\circ C$. Using the formula $\Delta T_f = i \cdot K_f \cdot m$:

$1.86^\circ C = 1 \cdot K_f \cdot 1 \text{ molal}$

$K_f = 1.86 \text{ K kg mol}^{-1}$

2. Calculate the van't Hoff factor ($i$) for the CH3COOH solution:

For the 0.01 molal CH3COOH solution, the depression in freezing point ($\Delta T_f$) is 0.02046°C. Using the formula $\Delta T_f = i \cdot K_f \cdot m$:

$0.02046 = i \cdot 1.86 \cdot 0.01$

$i = \frac{0.02046}{1.86 \cdot 0.01} = \frac{0.02046}{0.0186}$

$i = 1.1$

3. Determine the degree of dissociation ($\alpha$) for CH3COOH:

Acetic acid (CH3COOH) is a weak acid that dissociates as:

$\text{CH}_3\text{COOH} \rightleftharpoons \text{H}^+ + \text{CH}_3\text{COO}^-$

It dissociates into 2 ions ($n=2$). The relationship between the van't Hoff factor ($i$) and the degree of dissociation ($\alpha$) is:

$i = 1 + (n-1)\alpha$

$1.1 = 1 + (2-1)\alpha$

$1.1 = 1 + \alpha$

$\alpha = 1.1 - 1 = 0.1$

4. Calculate the concentration of H$^+$ ions:

The initial concentration of CH3COOH ($C$) is 0.01 molal. Assuming molality is equal to molarity, $C = 0.01$ M. The concentration of H$^+$ ions at equilibrium is given by:

$[\text{H}^+] = C \alpha$

$[\text{H}^+] = 0.01 \text{ M} \times 0.1$

$[\text{H}^+] = 0.001 \text{ M}$

$[\text{H}^+] = 10^{-3} \text{ M}$

5. Calculate the pH of the solution:

$\text{pH} = -\log[\text{H}^+]$

$\text{pH} = -\log(10^{-3})$

$\text{pH} = 3$