Question

The density of the core of a planet is ${\rho _1}$ and that of the outer shell is ${\rho _2}$ . The radii of the core and that of the planet are $R$ and $2R$ respectively. The acceleration due to gravity at the surface of the planet is the same as at a depth $R$ . The ratio of density $\frac{{{\rho _1}}}{{{\rho _2}}}$ will be:
(A) $7/3$
(B) $5/3$
(C) $8/3$
(D) $1/3$

Answer 1

To solve this question, we need to find out the gravitational field at the surface and at a point at the depth $R$ below the surface. Equating these, we will get the relation between the densities of the core and of the outer shell, from which the required ratio can be calculated.

Complete step-by-step solution
Consider the core and the outer shell of the planet as shown in the figure below.

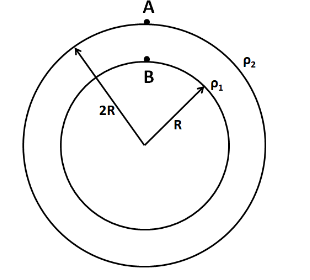
Consider the point A on the surface of the planet, and the point B at a depth of $R$ below the surface.
The acceleration due to gravity at the point A will be the sum of the acceleration due to gravity due to the outer shell and that due to the core, that is,
${g_A} = \dfrac{{G{M_1}}}{{{{\left( {2R} \right)}^2}}} + \dfrac{{G{M_2}}}{{{{\left( {2R} \right)}^2}}}$
${g_A} = \dfrac{{G{M_1} + G{M_2}}}{{4{R^2}}}$ .....................(1)
Now, the acceleration due to gravity at point B will be due to the core only since we know that the gravitational field inside a hollow spherical shell is equal to zero. So we have
${g_B} = \dfrac{{G{M_1}}}{{{R^2}}}$ .....................(2)
According to the question, the acceleration due to gravity at the surface of the planet is the same as that at the depth $R$ . So we have
${g_A} = {g_B}$
From (1) and (2)
$\dfrac{{G{M_1} + G{M_2}}}{{4{R^2}}} = \dfrac{{G{M_1}}}{{{R^2}}}$
Cancelling $\dfrac{G}{{{R^2}}}$ from both the sides, we have
$\dfrac{{{M_1} + {M_2}}}{4} = {M_1}$
$\Rightarrow {M_2} = 3{M_1}$ .....................(3)
Now, since the density of the core is given to be ${\rho _1}$ and is radius is equal to $R$ , so its mass can be written as
${M_1} = {\rho _1} \times \dfrac{4}{3}\pi {R^3}$ .....................(4)
Similarly, we can write the mass of the outer shell as
${M_2} = {\rho _2} \times \left( {\dfrac{4}{3}\pi {{\left( {2R} \right)}^3} - \dfrac{4}{3}\pi {R^3}} \right)$
$\Rightarrow {M_2} = \dfrac{4}{3}\pi {R^3}\left( {7{\rho _2}} \right)$ .....................(5)
Putting (4) and (5) in (3) we get
$\dfrac{4}{3}\pi {R^3}\left( {7{\rho _2}} \right) = 3{\rho _1} \times \dfrac{4}{3}\pi {R^3}$
Cancelling $\dfrac{4}{3}\pi {R^3}$ from both the sides, we get
$7{\rho _2} = 3{\rho _1}$
$\dfrac{{{\rho _1}}}{{{\rho _2}}} = \frac{7}{3}$
Thus, the ratio of $\dfrac{{{\rho _1}}}{{{\rho _2}}}$ is equal to $7/3$ .
Hence, the correct answer is option A.

Note
Do not consider the mass of the outer shell to be the mass of the whole of the bigger sphere of radius $2R$ . This is because the bigger sphere is composed of both the outer shell and the core. The outer shell is only the region outside the core.