Question
Question: The density of the core of a planet is \({{p}_{1}}\)and that of the outer shell is \({{p}_{2}}\). Th...
The density of the core of a planet is p1and that of the outer shell is p2. The radii of the core and that of the planets are R and 2R respectively. The acceleration due to gravity at the surface of the planet is the same as at a depth R. The ratio of density p1/p2 will be:
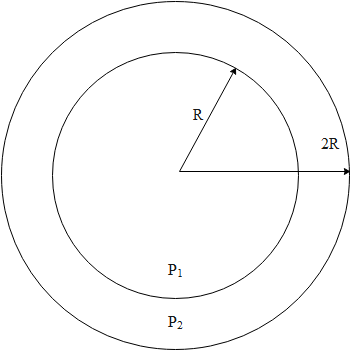
(A) 7/3
(B) 5/3
(C) 8/3
(D) 1/3
Solution
Hint Acceleration due to gravity is defined as the acceleration which is gained by an object due to the gravitational force. The SI unit is given as a meter per second square. Based on this concept we can solve this question.
Complete step by step answer
Suppose, the mass of the core of the planet is m and that of the outer shell is m.
So, the field on the surface of the core is R2Gm.
And, on the surface of the shell it will be (2R)2G(m+m/).
So, we can find that:
R2Gm=(2R)2G(m+m/)
So, we can say that:
4m=m+m/
⇒m/=3m
Let us consider that m=34πR3p1
So, we can evaluate that:
3m=3(34πR3p1)=m/=34π7R3p2
So, the value we get that:
p1=37p2
So, the ratio of p1/p2is given as 7/3.
Note We should know that the gravitational force depends on two factors : the mass and the distance. If the mass of one object is doubled then force of gravity between the objects also gets doubled. Increasing the distance, results in the lowering of the gravitational force.
