Question

The density of ice is $917kg{{m}^{-3}}$. What fraction of ice lies below water? The density of seawater is $1024kg{{m}^{-3}}$. What fraction of the iceberg do we see assuming that it has the same density as ordinary ice ($917kg{{m}^{-3}}$)?

Answer 1

Hint: Apply Archimedes’ principle. Draw the free body diagram, mention all the forces and do force balance then find a fraction of ice lying below water.

Complete step by step answer:
When a body is placed in a fluid, there is an upward force exerted on the body that upward force is equal to weight of the fluid displaced by it as it.
When this force is equal to the weight of the body then the net downward force acting on the body is zero and the body starts to float in the fluid.

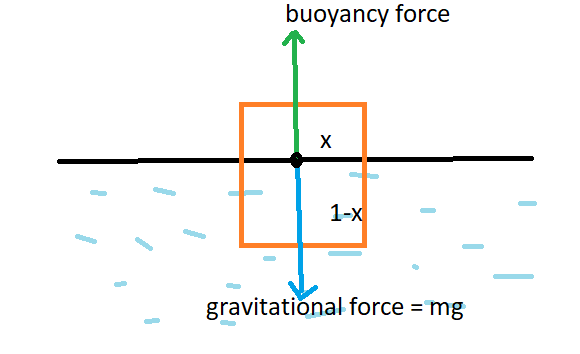
Let x = fraction of iceberg above water surface
1 – x = fraction of iceberg below water surface
V = volume of iceberg
Gravitational force = buoyancy force
$\begin{aligned} & {{\rho }_{iceberg}}Vg={{\rho }_{water}}(1-x)Vg \\\ & 917=1024(1-x) \\\ & 1-x=\dfrac{917}{1024} \\\ & 1-x=0.895 \\\ & x=0.105 \\\ \end{aligned}$
Hence, 0.895V that is 89.5 % of iceberg lies below water
And 10.5 % of the iceberg is visible.

Note: Always remember that buoyancy force is applied by fluid on the floating body. So for the value of mass, multiply density of fluid (not density of body) and volume of body inside the fluid Students sometimes do the opposite and can solve wrong.